Lors de mon précédent article, je vous ai montré comment implémenter la régression linéaire en utilisant une seule variable prédictive. Toutefois, une variable cible est généralement prédite non seulement avec une seule variable prédictive mais avec plusieurs. Dans ce cas, on parle de Multivariate Regression (régression linéaire multivariée). Dans cet article, on en implémentera une en utilisant les libraires de Machine learning de Python.
Multivariate Regression
Quand une variable cible est le fruit de la corrélation de plusieurs variables prédictives, on parle de Multivariate Regression pour faire des prédictions. Prenons, par exemple, la prédiction du prix d’une voiture. Le prix est la variable cible, les variables prédictives peuvent être : nombre de kilomètres au compteur, le nombre de cylindres, nombre de portes…etc. Toutes ces variables prédictives seront utilisées dans notre modèle de régression linéaire multivariée pour trouver une fonction prédictive.
Dans le cas de régression linéaire multivariée, la fonction prédictive s’écrira sous la forme :
A noter que :
-
- ε : est une constante
- α, β, γ…. : représente les coefficients de notre fonction prédictive F(X)
- X : est un vecteur/tableau de variables prédictives. Pour l’exemple de prédiction du prix de voiture, la taille du vecteur X sera égale à 3 (nombre de Km, nombre de cylindres, et le nombre de portes)
- xi : représente la ième variable prédictive.
Maintenant qu’on sait à quoi ressemblera notre fonction prédictive ainsi que nos données, essayons d’appliquer ce concept dans un cas concret en le codant en Python.
Présentation du problème
Supposons que je souhaite vendre ma maison qui se trouve à Portland aux États-Unis. Pour déterminer un bon prix, je dispose des données de prix de vente effectuées dans le passé dans la même ville. Ainsi, pour chaque maison vendu (une observation), je dispose des données suivantes :
- La taille de la superficie en pieds2
- Le nombre de chambre de la maison
- Le prix auquel elle a été vendu
| Taille en pieds2 | nombre de chambres | prix de vente en $ |
|---|---|---|
| 2104 | 3 | 329900 |
| 1600 | 3 | 329900 |
| 2400 | 3 | 369000 |
| 1416 | 2 | 232000 |
Le jeu de données comporte 47 enregistrements.
Note 1 : Un pieds² fait environ 0,092 m²
Note 2 : Le fichier de données est sous forme Excel, et est téléchargeable depuis mon espace Github
Chargement des données
Pour commencer, il faudra lire et charger les données contenues dans le fichier Excel. Python propose via sa librairie Pandas des classes et fonctions pour lire divers formats de fichiers notamment les fichiers Excel.
import pandas as pd
df = pd.read_excel("D:\DEV\PYTHON_PROGRAMMING\coursera_ml_exercices_in_python\Multivariate_Linear_Regression_dataset.xlsx")
La fonction read_excel(), renvoie un DataFrame, Il s’agit d’un tableau de trois dimensions contenant respectivement : la taille de la maison, le nombre de chambres et le prix auquel elle a été vendu.
Pour afficher les premières lignes chargées depuis notre fichier excel, on peut utiliser :
print df.head()
Nous devons ensuite séparer la variable cible (Y) des variables prédictives xi. Pour se faire :
# Récupérer l'ensemble des valeurs de la variable cible Y = df["prix"] # Récupérer les variables prédictives (on en a 2) X = df[['taille_en_pieds_carre','nb_chambres']]
Représentation des données
Pour mieux comprendre les données, il est souvent utile de les visualiser. Ici, nous avons un jeu de données de 3 dimensions. Nos données seront éparpillées dans un espace 3D (chaque ligne du dataset sera un couple (x,y,z)). On peut représenter les données dans un espace 3D avec la librairie matplotlib :
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(1,2,1, projection='3d')
ax.scatter(df["taille_en_pieds_carre"], df["nb_chambres"], df["prix"], c='r', marker='^')
ax.set_xlabel('surface en pieds_carre')
ax.set_ylabel('nb_chambres')
ax.set_zlabel('prix en $')
plt.show()
Ce qui nous donnera le « scatter plot » 3D:
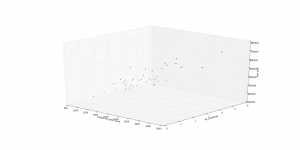
Normalisation des données et feature Scaling
Vous l’avez peut être remarqué, notre exemple comporte des variables prédictives avec des ordres de grandeurs très différents. En effet, le nombre de chambre d’une maison est généralement compris entre 1 et 10 alors que la superficie se compte en quelques milliers de pieds2.
Pour appliquer l’algorithme Multivariate Regression, il est nécessaire que les variables prédictives faisant partie du modèle prédictif soient du même ordre de grandeur. Généralement, il faut que la valeur de chaque variable prédictive soient compris (approximativement) entre -1 et 1. Si certaines valeurs dépassent un peu (par exemple -2 , 1.5…) ce n’est pas très grave.
Pour ramener nos variables prédictives au même ordre de grandeur, nous appliquerons un procédé qui s’appelle : features scaling
Note : Je suis conscient que je n’ai pas bien détaillé la raison d’application du feature scaling. Je ferai un billet de blog dédié à ce sujet pour en expliquer les motivations derrières ainsi que la formule mathématique pour faire du feature scaling sur une variable prédictive. Pour le moment, retenez juste que quand vous avez des variables prédictives avec des ordres de grandeurs différents, il faudra appliquer le feature scaling.
La librairie Scikit learn de Python propose plusieurs classes et méthodes pour faire de la préparation de données (Data pre-processing) pour les algorithmes de Machine Learning. Le package sklearn.preprocessing propose la classe StandardScaler qui permettra de faire du features scaling sur toutes nos variables prédictives.
from sklearn.preprocessing import StandardScaler scale = StandardScaler() X_scaled = scale.fit_transform(X[['taille_en_pieds_carre', 'nb_chambres']].as_matrix())
Après le feature scaling, voici à quoi ressemble nos données :
Out[139]:
array([[ 1.31415422e-01, -2.26093368e-01],
[ -5.09640698e-01, -2.26093368e-01],
[ 5.07908699e-01, -2.26093368e-01],
[ -7.43677059e-01, -1.55439190e+00],
[ 1.27107075e+00, 1.10220517e+00],
....
[ -1.89112638e-01, 1.10220517e+00],
[ -1.01459959e+00, -2.26093368e-01]])
Apprentissage de l’algorithme par les données
On y est ! tous les ingrédients sont là pour pouvoir appliquer notre algorithme de régression linéaire multivariée. Parmi les procédés mathématiques pour faire de la régression linéaire, il y a le Ordinary Least Squares (OLS).
Définition Wikipedia (anglais):
Ordinary least squares (OLS) or linear least squares is a method for estimating the unknown parameters in a linear regression model, with the goal of minimizing the sum of the squares of the differences between the observed responses (values of the variable being predicted) in the given dataset and those predicted by a linear function of a set of explanatory variables.
En d’autres termes, OLS est une méthode pour estimer une variable cible dans un modèle de régression linéaire. Pour y parvenir, OLS va minimiser la somme des carrés des différences entre les réponses observées (de notre Training Set) et ceux prédits par la fonction linéaire appliquée à nos variables prédictives de notre ensemble de données.
Rassurez vous, vous n’aurez pas à comprendre comment fonctionne Ordinary Least Squares. il vous suffira de savoir que c’est un estimateur que nous pourrons utiliser ici pour notre problème. Et tout ça pour dire que Python, propose une implémentation de OLS via son package statsmodels.api
est = sm.OLS(Y, X).fit() print est.summary()
Ceci nous affiche un résumé sur le modèle prédictif produit :
OLS Regression Results
==============================================================================
Dep. Variable: prix R-squared: 0.966
Model: OLS Adj. R-squared: 0.964
Method: Least Squares F-statistic: 631.4
Date: Wed, 26 Apr 2017 Prob (F-statistic): 1.19e-33
Time: 00:40:23 Log-Likelihood: -589.11
No. Observations: 47 AIC: 1182.
Df Residuals: 45 BIC: 1186.
Df Model: 2
Covariance Type: nonrobust
=========================================================================================
coef std err t P>|t| [0.025 0.975]
-----------------------------------------------------------------------------------------
taille_en_pieds_carre 140.8611 15.355 9.174 0.000 109.935 171.788
nb_chambres 1.698e+04 1.01e+04 1.676 0.101 -3424.632 3.74e+04
==============================================================================
Omnibus: 2.046 Durbin-Watson: 1.923
Prob(Omnibus): 0.359 Jarque-Bera (JB): 1.215
Skew: 0.354 Prob(JB): 0.545
Kurtosis: 3.346 Cond. No. 2.17e+03
==============================================================================
Visualisation de la fonction de prédiction
On dispose maintenant de notre modèle prédictif, nous pourrons réutiliser notre training Set pour « dessiner » la fonction prédictive qu’on a obtenu. Vu qu’on dispose d’un ensemble de données de 3 dimensions, la fonction obtenue sera également définie dans un espace 3D. Pour rappel, notre fonction prédictive est définie comme suit :
prix_estimé = F(superficie, nb_chambres) = ε + α * superficie + β * nb_chambres
Nous pourrons appliquer cette fonction sur les données qu’on a utilisées pour l’entrainement d’OLS, pour obtenir un ensemble de prédictions de prix :
def predict_price_of_house(taille_maison, nb_chambre):
#return 140.8611 * taille_maison + 1.698e+04 * nb_chambre
Et on dessine le tout dans un plan 3D, par ce code Python :
def predict_all(lst_sizes, lst_nb_chmbres):
predicted_prices = []
for n in range(0, len(Y)):
predicted_prices.append(predict_price_of_house(lst_sizes[n], lst_nb_chmbres[n]))
return predicted_prices
ax = fig.add_subplot(1, 2, 2, projection='3d')
ax.plot_trisurf(df[\"taille_en_pieds_carre\"], df["nb_chambres"], predict_all(df["taille_en_pieds_carre"], df["nb_chambres"]))
plt.show()
et Voila !
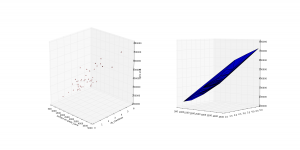
Note : Il aurait été plus pertinent de fusionner les deux figures dans une seule pour mieux visualiser comment les prédictions sont proches des prix réels. Malheureusement, je n’ai pas réussi à le faire avec Matplotlib 3D.
Test de prédiction
Nous pourrons utiliser notre modèle prédictif pour prédire le prix d’une maison qui n’est pas présente dans notre jeu de données. Estimons, le prix d’une maison avec 4500 pieds² et avec 5 chambres :
print predict_price_of_house(4500,5) # ce qui donne : 718774.95 $
On remarque que le prix prédit n’est pas très éloigné du prix de maisons à caractéristiques similaires. Nous pourrons dire que nous avons un bon estimateur de prix ! 🙂
>> Téléchargez le code source depuis mon espace Github <<
Résumé
Dans cet article, nous venons d’implémenter Multivariate Regression en Python. Notamment en utilisant la technique OLS. Nous avons vu comment visualiser nos données par des graphes, et prédire des résultats.
Nous avons abordé la notion de feature scaling et de son cas d’utilisation dans un problème de Machine Learning. Cette notion fera l’objet d’un article plus détaillé.
Si vous avez des questions, n’hésitez pas à me les poser dans un commentaire et si l’article vous plait, n’oubliez pas de le faire partager ! 😉

Bonjour Younes,
Je voudrais te demander quelques questions:
Je travail actuellement sur un TP de régression linéaire à deux variables qui ressemble beaucoup à l’exemple dans ton article .
La première partie c’est de prédire le prix d’un loyer Y en fonction de la surface X (jusqu’ici ça va!)
La deuxième partie je dois prendre en compte une nouvelle variable(l’arrondissement) donc X(surface,arrondissement) .
Pour le deuxième cas j’ai appliqué la régression linéaire bivariée j’obtient un bon score dans
la prédiction par contre le coefficient associé à l’arrondissement toujours négatif.
J’ai du mal à interpréter ce résultat.
Je remarque deux choses :
– la variable surface est quantitative et l’arrondissement est qualitative.
– Les ordres de grandeurs des deux variables explicatives sont très différentes. En effet La variable arrondissement prend des valeurs dans {1,2,3,4,10} . Est ce que je dois faire un features scaling comme expliqué dans ton article ?
Est-ce que ça explique ce coefficient négatifs? Ou tout simplement l’ajout de la variable arrondissent n’a aucun sens ici?
Merci pour ton aide.
Bonjour Siradio,
Lorsque tu fais de l’analyse de régression (Regression Analysis), il faut garder à l’esprit deux choses essentielles :
• Les données prédictives (les X) doivent être des valeurs continues (continuous data), comme par exemple la taille d’une personne
• Les modèles de régression supposent que les variables X sont indépendantes (bien que dans la vraie vie, ce n’est pas le cas)
Je te conseille également de lire mon article sur les différents types de données :
https://mrmint.fr/types-de-donnees-machine-learning
Lors de la régression linéaire, on veut des données continues parce que cela permet d’avoir un « ordre » naturel pour les valeurs, notamment on pourra dire que 1.57 > 1.2 (par exemple).
Certains praticiens de data science admettent l’utilisation des variables ordinales (comme la notation d’un film, on peut dire qu’un film 5 étoiles et « mieux » qu’un film 1 étoile).
Pour le cas des arrondissements, on ne peut pas appliquer ce genre de logique. Généralement, on déconseille d’utiliser ce genre de variables dans le modèle prédictifs (car il s’agit de Categorical Data).
Toutefois, si cela est vraiment nécessaire (je pense que c’est hors cadre de ton TP), il existe une méthode nommé « dummy variables » qui permet d’inclure les « categorical data », Je te conseille de lire ce pdf:
https://www.moresteam.com/whitepapers/download/dummy-variables.pdf
Interprétation des poids (weights) de ton modèle :
Tu peux voir la valeur des poids de ton modèle prédictif comme le degré d’importance que le modèle prédictif accorde à une feature X. Plus la valeur est grande, plus cette feature est importante et contribue fortement à la prédiction finale. Et vice versa. Donc il n’est pas choquant que tu aies des poids négatifs pour ton modèle prédictif.
Finalement, le feature Scaling doit s’appliquer du moment que l’ordre de grandeur des variables est important.
J’espère que ces réponses t’aident à avancer dans ton TP 🙂
Bonjur Younes,
C’est parfait! Merci beaucoup c’est très claire tes explications.
Merci Merci !!
A très bientôt !
Bonjour Younes,
Tout d’abord merci pour ce fabuleux site!
,j’ai bien démarré en ML grâce à tous vos articles. C’est juste agréable 🙂
Je viens de finir de tester le code et juste à la fin je commence à bidouiller la fonction fig.add pour mieux comprendre l’affichage et bim j’arrive à afficher les deux figures! j’ai just changer le premier appel ainsi
ax = fig.add_subplot(1,1,1, projection=’3d’)
puis j’ai désactivé le deuxième appel
#ax = fig.add_subplot(1, 2, 2, projection=’3d’)
et voilà j’ai eu les deux figures ensmble et je me suis dis que ça sera bien de le partager avec vous!
Encore merci
Amine
Bonjour Amine,
Je vous remercie pour votre retour, je vais inclure tes modifications dans les sources et mettre à jour le code pour que tout le monde en profit 😉
Younes
Merci pour vos cours c magnifique vous avez bien expliquer plusieurs choses qu’on etait flou pour moi pour ce chapitre j’ai essayée votre code mais j’ai envisagée un petit probleme au niveau du feature scaling en faite sa m’affiche un erreur d’attribue a cause de « as.matrix() » et quand jai supprimer se dernier sa fonctionner normalement je voudrais savoir si cette changement va causer un probleme ou pas et merci 🙂
Bonjour,
Merci pour le commentaire 🙂
Je ne sais pas quelle version des librairies vous utilisez, mais si vous optez sur les mêmes prédictions c’est que tout est bon.
Bon courage