Lors de mon article précédent, on a abordé l’algorithme K-Means. Il s’agit d’un algorithme de clustering populaire en apprentissage non-supervisé.

Lors de cet article, on verra comment appliquer l’algorithme K-Means sur un vrai jeu de données en se basant sur la librairie Scikit Learn.

C’est parti !

Prérequis :

Avant d’attaquer le vif du sujet, sachez qu’il faut disposer d’un certain nombre de prérequis :

• Avoir Python 3 sur son poste
• Importer les bibliothèques nécessaires  pandas , numpy ,matplotlib et scikit learn.
• Disposer de Jupyter pour les notebooks Python.

Si vous vous connaissez bien en Python, vous pouvez installer manuellement ces prérequis. Sinon le plus simple est d’installer Anaconda qui vient avec la version 3 de Python. Vous pouvez lire mon article sur l’installation d’Anaconda pour réussir la configuration de ce dernier.

Choix du data set

Présentation du Jeu de données Iris 

Le jeu de données Iris a été initialement publié à l’ UCI Machine Learning Repository: Iris Data Set. Ce Data Set de 1936 est souvent utilisé pour tester des algorithmes d’apprentissage automatique et des visualisations.

Le jeu de données Iris contient trois variantes de la fleur Iris. Il contient 150 instances (ligne du jeu de donnée). Chaque instance est composée de quatre attributs pour décrire une fleur d’Iris. Le jeu de données est étiquetée par le type de fleur. Ainsi pour quatre attributs décrivant une fleur d’Iris, on saura de quelle variante il s’agit.

Finalement, le jeu de données ne contient pas de valeurs manquantes. Ce qui nous dispense de les traiter.

Note : Vous pouvez lire cet article sur comment représenter les données en Machine Learning pour vous aider à comprendre comment le jeu de données Iris se compose.

Implémentation de K-Means 

Lors de cette section, je vais décrire les fonctionnements des différents snippets de code qui m’ont permis d’utiliser K-Means sur le jeu de données Iris. Vous pourrez retrouver l’intégralité du code à télécharger sur mon espace Github.

Import des librairies nécessaires

Premièrement, nous importons les bibliothèques pandas ,numpy, pyplot et sklearn .

#import des librairies l'environnement
import pandas as pd
import numpy as np
import sklearn.metrics as sm
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn import datasets

Depuis la librairie Scikit Learn, on a besoin de  KMeans. On le charge depuis le sous module module cluster de sklearn.

Chargement des données

La librairie Sickit Learn offre des méthodes utilitaires pour charger des jeux de données populaires comme celui d’Iris. Ces méthodes se retrouvent dans la classe datasets.

Pour charger notre jeu de données Iris, on utilise la méthode load_iris().

#chargement de base de données iris
iris = datasets.load_iris()

Vous pouvez afficher les données en exécutant chaque ligne individuellement.

#affichage des données, vous permet de mieux comprendre le jeu de données (optionnel) 
print(iris)
print(iris.data)
print(iris.feature_names)
print(iris.target)
print(iris.target_names)

Utilisation de la librairie Pandas

Pandas est une librairie assez utilisée quand on fait du Machine Learning avec Python. Grâce à sa classe DataFrame, on peut manipuler aisément les données en format tabulaire.

#Stocker les données en tant que DataFrame Pandas 
x=pd.DataFrame(iris.data)
# définir les noms de colonnes
x.columns=['Sepal_Length','Sepal_width','Petal_Length','Petal_width']
y=pd.DataFrame(iris.target)
print(y.columns=['Targets'])

Notez que nous avons séparé le jeu de données en deux variables :

• La variable 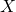contient les observations, il s’agit d’une matrice de taille 150*4
• Les étiquettes sont dans une variable

 

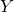
Construction du modèle K-means

Maintenant qu’on a mis les données dans le bon format (dans un Data Frame), l’entrainement de K-Means est facilité avec la librairie Scikit-Learn.

Il suffit d’instancier un objet de la classe kmeans en lui indiquant le nombre de clusters qu’on veut former. Par la suite il faut appeler la méthode fit() pour calculer les clusters.

#Cluster K-means
model=KMeans(n_clusters=3)
#adapter le modèle de données
model.fit(x)

Rappelez-vous, que lors d’un apprentissage non supervisé, l’algorithme n’a pas d’étiquette . Il découvre des patterns en fonction des caractéristiques se trouvant dans la matrice . Pour notre cas, K-Means ne sait pas que la première fleur Iris de notre jeu de données est de telle ou telle variante.

Le snippet de code ci-dessous permet d’afficher le clustering fait par l’algorithme K-Means :

print(model.labels_)

Le tableau qu’on voit  ci-dessous représente le numéro de cluster affecté à chaque fleur. Vu qu’on a demandé un regroupement en trois clusters, on en a trois intitulé cluster 0, cluster 1, cluster 2. Ainsi, la dernière fleur  fait partie du 3ème cluster (cluster 2) et la première fait partie du 1er cluster (cluster 0).

array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 1, 1, 1, 1, 2, 1, 1, 1,
       1, 1, 1, 2, 2, 1, 1, 1, 1, 2, 1, 2, 1, 2, 1, 1, 2, 2, 1, 1, 1, 1,
       1, 2, 1, 1, 1, 1, 2, 1, 1, 1, 2, 1, 1, 1, 2, 1, 1, 2])

Visualisez les résultats du classificateur

Le tableau ci-dessus nous fournit quelle appartenance de chaque fleur à quelle cluster. Toutefois, un tableau de la sorte n’est pas très parlant. Vu que notre jeu de données est relativement petit, on peut visualiser graphiquement notre jeu de données pour observer les clusters formés.

 

plt.scatter(x.Petal_Length, x.Petal_width)

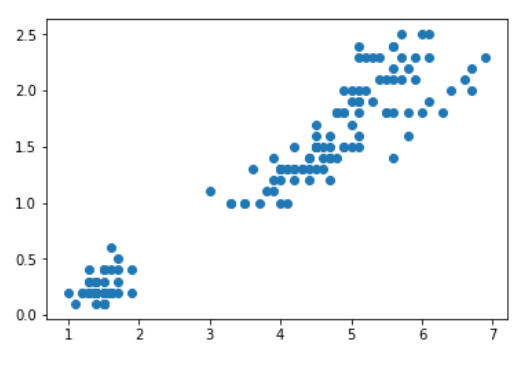
Figure 1 : Répartition de l’Iris Dataset dans un scatter plot 2D

En nous basant sur la longueur et la largeur de chaque pétale, on peut afficher, dans un plan 2D, les différentes fleurs de notre jeu de données. Visuellement, on voit qu’il y a deux grands groupes qui se forment.

Ici, nous traçons la longueur et la largeur des pétales, mais chaque tracé change les couleurs des points en utilisant soit  colormap [y.Targets] pour la classe originale et colormap [model.labels_] pour la classe prédite.

colormap=np.array(['Red','green','blue'])
plt.scatter(x.Petal_Length, x.Petal_width,c=colormap[y.Targets],s=40)
plt.scatter(x.Petal_Length, x.Petal_width,c=colormap[model.labels_],s=40)

Le code ci-dessus produit deux scatter plots. Le premier affiche les fleurs selon leurs classes. Ainsi, les fleurs Iris ayant une classe seront de couleur rouge, et celles de classe seront vertes et celles de classe seront de couleur bleu.

Le résultat graphique est le suivant :

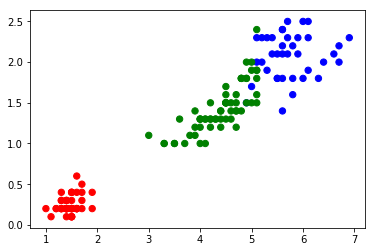
Figure 2 : Scatter plot des fleurs Iris en fonction de leurs variantes

 

nous pouvons voir que le classificateur K-means a identifié une classe correctement (en rouge) mais certains bleus ont été classés comme verts et vice versa.

Le second appel à la méthode plt.scatter() en utilisant la variable model.labels_ permet d’afficher les différents clusters créés par K-Means. Rappelez-vous model.labels_ est un tableau contenant les affectations de chaque classe à un cluster (section : construction du modèle K-Means).

 

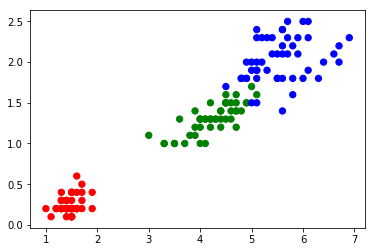
Figure 3 : Clustering de 3 classes du Iris Dataset

On remarque que les clusters formés dans la figure 3 sont proches de ceux de la figure 2 qui représente la « vraie » répartition des données Iris en fonction de leurs étiquettes.

Ainsi, on remarque que les algorithmes de Clustering (pour notre cas K-Means) permettent de répartir en groupes des jeux de données en fonction de leurs caractéristiques et ce, sans avoir besoin de leurs étiquettes (variable ) correspondante.

 

>> Téléchargez le code source depuis mon espace Github <<

 

Conclusion

Dans cet article, vous avez appris comment utiliser l’algorithme K-Means de la librairie Scikit-Learn. Cette dernière rend son application aisée et facile.

A vous de reprendre le code et de tester un nombre de clusters différents et voir ce qui en ressort comme partitionnement. N’hésitez pas à partager vos découvertes par un commentaire !

Finalement, Si vous avez des questions n’hésitez pas à me les poser par commentaire. J’y répondrai du mieux que je peux. 🙂