K-means (k-moyennes) est un  algorithme non supervisé  de clustering, populaire en Machine Learning. Lors de cet article, nous allons détailler son fonctionnement et dans quel cas d’usage il peut être appliqué.

Qu’est ce que le clustering

Le clustering est une méthode d’apprentissage non supervisé (unsupervised learning). Ainsi, on n’essaie pas d’apprendre une relation de corrélation entre un ensemble de features d’une observation et une valeur à prédire , comme c’est le cas pour l’apprentissage supervisé. L’apprentissage non supervisé va plutôt trouver des patterns dans les données. Notamment, en regroupant les choses qui se ressemblent.

En apprentissage non supervisé, les données sont représentées comme suit :

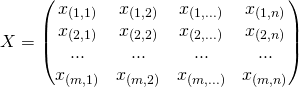
Chaque ligne représente un individu (une observation). A l’issu de l’application du clustering, on retrouvera ces données regroupées par ressemblance. Le clustering va regrouper en plusieurs familles (clusters) les individus/objets en fonction de leurs caractéristiques. Ainsi, les individus se trouvant dans un même cluster sont similaires et les données se trouvant dans un autre cluster ne le sont pas.

Il existe deux types de clustering :

• Le clustering hiérarchique
• Le clustering non-hiérarchique (partitionnement)

J’élaborerai la différence entre ces deux concepts lors d’un autre article. Pour le moment, retenez juste, que le concept de clustering tel que je l’ai décrit lors de ce paragraphe est un clustering non hiérarchique.

Qu’est ce que K-means

K-means est un algorithme non supervisé de clustering non hiérarchique. Il permet de regrouper en  clusters distincts les observations du data set. Ainsi les données similaires se retrouveront  dans un même cluster. Par ailleurs, une observation ne peut se retrouver que dans un cluster à la fois (exclusivité d’appartenance). Une même observation, ne pourra donc, appartenir à deux clusters différents.

Notion de similarité

Pour pouvoir regrouper un jeu de données en cluster distincts, l’algorithme K-Means a besoin d’un moyen de comparer le degré de similarité entre les différentes observations. Ainsi, deux données qui se ressemblent, auront une distance de dissimilarité réduite, alors que deux objets différents auront une distance de séparation plus grande.

Les littératures mathématiques et statistiques regorgent de définitions de distance, les plus connues pour les cas de  clustering sont :

• La distance Euclidienne : C’est la distance géométrique qu’on apprend au collège. Soit une matrice 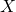à 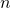variables quantitatives. Dans l’espace vectoriel 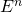. La distance euclidienne 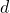entre deux observations 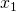et 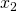se calcule comme suit :

• La distance de Manhattan (taxi-distance) : est la distance entre deux points parcourue par un taxi lorsqu’il se déplace dans une ville où les rues sont agencées selon un réseau ou un quadrillage. Un taxi-chemin est le trajet fait par un taxi lorsqu’il se déplace d’un nœud du réseau à un autre en utilisant les déplacements horizontaux et verticaux du réseau. (source wikipedia.)

 

Choisir K : le nombre de clusters

Choisir un nombre de cluster K n’est pas forcément intuitif. Spécialement quand le jeu de données est grand et qu’on n’ait pas un a priori ou des hypothèses sur les données. Un nombre grand peut conduire à un partitionnement trop fragmenté des données. Ce qui empêchera de découvrir des patterns intéressants dans les données. Par contre, un nombre de clusters trop petit, conduira à avoir, potentiellement, des cluster trop généralistes contenant beaucoup de données. Dans ce cas, on n’aura pas de patterns « fins » à découvrir.

Pour un même jeu de données, il n’existe pas un unique clustering possible. La difficulté résidera donc à choisir un nombre de cluster qui permettra de mettre en lumière des patterns intéressants entre les données. Malheureusement il n’existe pas de procédé automatisé pour trouver le bon nombre de clusters.

La méthode la plus usuelle pour choisir le nombre de clusters est de lancer K-Means avec différentes valeurs de et de calculer la variance des différents clusters.  La variance est la somme des distances entre chaque centroid d’un cluster et les différentes observations inclues dans le même cluster. Ainsi, on cherche à trouver un nombre de clusters de telle sorte que les clusters retenus minimisent la distance entre leurs centres (centroids) et les observations dans le même cluster. On parle de minimisation de la distance intra-classe.

La variance des clusters se calcule comme suit :

Avec :

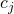• : Le centre du cluster (le centroïd)
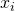• : la ième observation dans le cluster ayant pour centroïd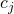
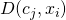• : La distance (euclidienne ou autre) entre le centre du cluster et le point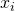

Généralement, en mettant dans un graphique les différents nombres de clusters en fonction de la variance, on retrouve un graphique similaire à celui-ci :

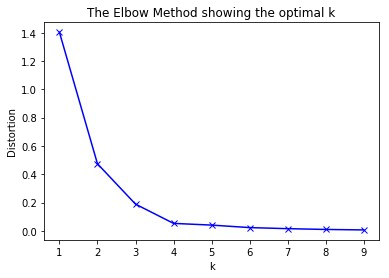On remarque sur ce graphique, la forme d’un bras où le point le plus haut représente l’épaule et le point où vaut 9 représente l’autre extrémité : la main. Le nombre optimal de clusters est le point représentant le coude. Ici le coude peut être représenté par valant 2 ou 3. C’est le nombre optimal de clusters. Généralement, le point du coude est celui du nombre de clusters à partir duquel la variance ne se réduit plus significativement. En effet, la « chute » de la courbe de variance  (distortion) entre 1 et 3 clusters est significativement plus grande que celle entre 5 clusters et 9 clusters.

Le fait de chercher le point représentant le coude, a donné nom à cette méthode : La méthode Elbow (coude en anglais).

Finalement, le choix (au vu de ce graphique), entre 2 ou 3 clusters, reste un peu flou et à votre discrétion. Le choix se fera en fonction de votre jeu de données et ce que vous cherchez à accomplir. Finalement, Il n’y a pas de solution unique à un problème de clustering.

Cas d’utilisation K-means

K-Means en particulier et les algorithmes de clustering de façon générale ont tous un objectif commun : Regrouper des éléments similaires dans des clusters.  Ces éléments peuvent être tous et n’importe quoi, du moment qu’ils sont encodés dans une matrice de données.

Les champs d’application de K-Means sont nombreux, il est notamment utilisé en :

• la segmentation de la clientèle en fonction d’un certain critère (démographique, habitude d’achat etc….)
• Utilisation du clustering en Data Mining lors de l’exploration de données pour déceler des individus similaires. Généralement, une fois ces populations détectées, d’autres techniques peuvent être employées en fonction du besoin.
• Clustering de documents (regroupement de documents en fonction de leurs contenus. Pensez à comment Google Actualités regroupe des documents par thématiques.)

Fonctionnement de l’algorithme K-Means

k-means est un algorithme itératif qui minimise la somme des distances entre chaque individu et le centroïd. Le choix initial des centroïdes conditionne le résultat final.
Admettant un nuage d’un ensemble de points, K-Means change les points de chaque cluster jusqu’à ce que la somme ne puisse plus diminuer. Le résultat est un ensemble de clusters compacts et clairement séparés, sous réserve de choisir la bonne valeur   du nombre de clusters .

Principe algorithmique

Algorithme K-means

Entrée : 

• K le nombre de cluster à former
• Le Training Set (matrice de données)

DEBUT

Choisir aléatoirement K points (une ligne de la matrice de données). Ces points sont les centres des clusters (nommé centroïd).

                      REPETER

Affecter chaque point (élément de la matrice de donnée) au groupe dont il est le plus proche au son centre

Recalculer le centre de chaque cluster  et modifier le centroide

                     JUSQU‘A     CONVERGENCE

                               OU    (stabilisation de l’inertie totale de la population)

FIN ALGORITHME

Note 1: Lors de la définition de l’algorithme, quand je parle de « point », c’est un point au sens « donnée/data » qui se trouve dans un espace vectoriel de dimension . Avec : le nombre de colonnes de la matrice de données.

Note 2 : La convergence de l’algorithme K-Means peut être l’une des conditions suivantes :

• Un nombre d’itérations fixé à l’avance, dans ce cas, K-means effectuera les itérations et s’arrêtera peu importe la forme de clusters composés.
• Stabilisation des centres de clusters (les centroids ne bougent plus lors des itérations).

L’affectation d’un point   à un cluster se fait en fonction de la distance de ce point par rapport aux différents centroides. Par ailleurs, ce point se fera affecté à un cluster s’il est plus proche de son centroid (distance minimale). Finalement, la distance entre deux points dans le cas de K-Means se calcule par les méthodes évoquées dans le paragraphe « notion de similarité ».

Remarques sur le K-Means

Optimums locaux

En analysant la façon de procéder de l’algorithme de K-means, on remarque que pour un même jeu de données, on peut avoir des partitionnements différents. En effet, L’initialisation des tous premiers centroids est complétement aléatoire. Par conséquent l’algorithme trouvera des clusters différents en fonction de cette première initialisation aléatoire. De ce fait, la configuration des clusters trouvés par K-Means peut ne pas être la plus optimale. On parle d’optimum local.

Afin de palier aux problèmes des optimums locaux, il suffit de lancer K-means plusieurs fois sur le jeu de données  (avec le même nombre de clusters et des initialisations initiales des centroids différentes) et voir la composition des clusters qui se forment. Par la suite garder celui qui convient à votre besoin.

 

Résumé

Dans cet article, vous avez découvert le principe de fonctionnement de K-Means. Il s’agit d’un algorithme d’apprentissage non supervisé dédié au clustering non hiérarchique.

Vous connaissez maintenant :

• Ce que c’est l’algorithme  K-Means
• Les cas où vous pouvez  utiliser K-Means
• Comment fonctionne cet algotithme ainsi que ses forces et ses limitations.

Finalement , j’espère que cet article pourra vous aider ,si vous avez des questions n’hésitez pas à me les poser par commentaire. J’y répondrai du mieux que je peux. 🙂