Dans les projets de Data Science, les données comportent souvent des valeurs aberrantes et des données manquantes (missing Data).
Il est important d’identifier les données manquantes dans un jeu de données avant d’appliquer un algorithme de Machine Learning (ML). En effet, beaucoup de ces derniers reposent sur des méthodes statistiques qui supposent recevoir un jeu de données complet en entrée. Faute de quoi, l’algorithme ML risque de fournir un mauvais modèle prédictif ou pire, ne pas fonctionner tout simplement. Ainsi, traiter les données manquantes est une phase nécessaire pour tout projet de Data Science.
Lors de cet article, on verra :
- Le problème des données manquantes en Data Science
- Les différents patterns d’absence de données (Missingness Patterns)
- Quelques techniques pour traiter les données manquantes
C’est parti !

Qu’est ce qu’une donnée manquante
Les algorithmes de Machine Learning prennent les données d’entrée (input Data) sous forme matricielle, chaque ligne est une observation, et chaque colonne représente une caractéristique (feature) de l’indivu (son salaire, appartenance politique etc…).
On dit qu’une observation (ligne de la matrice de données) comporte une donnée manquante s’il existe une feature pour laquelle sa valeur n’est pas renseignée. Evidemment, on peut avoir plusieurs données manquantes pour une même observation.
Les différents patterns d’absence de données
Les données manquantes sont un problème qui se manifeste non seulement en Data Science mais également en modélisation statistique. Toutefois, la préoccupation reste la même. A savoir, comment traiter ces données manquantes de façon à remplir les informations non renseignées et ce, sans altérer significativement le jeu de données initial.
La difficulté pour traiter les données manquantes réside dans les hypothèses que nous nous faisant à l’égard des patterns d’absence de données. Dans leurs ouvrage Statistical Analysis with Missing Data, Little et Rubin définissent trois patterns d’absence de données (Data Missingness Patterns).
Les données Missing Completely At Random (MCAR)
Quand la valeur d’une variable explicative (feature) X est manquante, on dit que cette feature est MCAR (Missing Completly At Random) si et seulement si la probabilité que la valeur soit manquante est indépendant des valeurs prises par les autres variables explicatives de l’observation, qu’elles soient manquantes ou non.
Plus formellement, on écrit :
Exemple :
Imaginons qu’on ait un jeu de données avec deux features: le prénom d’un individu et son sexe. Supposons que pour une observation, on a le prénom Paul mais la valeur du sexe n’est pas renseigné. Depuis la valeur du prénom « Paul », on peut déduire qu’il s’agit d’un homme. Dans ce cas, la variable explicative Sexe n’est pas MCAR.
Toujours avec le même exemple, supposons qu’on a une troisième feature « Salaire », et qu’on a l’observation : (Alice, Femme) et le salaire d’Alice n’est pas renseigné. La feature Salaire est MCAR car on ne peut savoir à l’avance si la valeur du salaire d’Alice sera renseignée ou non juste en se basant sur la prénom « Alice » et le fait qu’elle soit une femme.
Missing At Random (MAR)
On dit que les données manquantes d’une feature X sont Missing At Random (MAR) si et seulement si, la probabilité qu’une valeur X soit manquante est corrélée à l’existence de variables explicatives dont les valeurs sont renseignées. Par contre cette probabilité n’est pas corrélée à l’absence de valeurs de variables explicatives.
Plus formellement on écrit :
Tordu, non !? 😕
Clarifions cette définition par un exemple. Imaginons le jeu de données suivant :
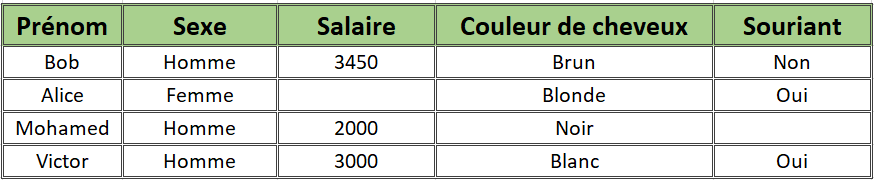
Les features de ce jeu de données sont :
- Prénom : le prénom d’un individu
- Sexe : représente le sexe d’une personne
- Salaire : Le salaire mensuel de l’individu
- Souriant : Le fait qu’il soit plutôt souriant ou non.
On dit que la variable (feature) Salaire est Missing At Random (MAR), Si l’absence d’une valeur dépend d’un attribut observé. Pour notre exemple, on voit que Alice qui est une Femme, n’a pas renseigné son salaire. On peut supposer la probabilité que la feature Salaire soit absente est corrélée à la présence de la variable Sexe.
Toutefois l’inverse n’est pas vrai, imaginons qu’on a une observation d’une personne dont on ne connait pas le sexe. D’un point de vue de probabiliste, on est incapable de dire si la variable salaire pour cet individu sera présente ou non.
Not Missing At Random (NMAR)
la probabilité qu’une valeur d’une variable explicative soit manquante ou pas, ne dépend que d’elle même et n’est corrélée avec aucune des valeurs des autres variables explicatives. En d’autre terme, il existe un pattern qui motive l’absence d’une valeur.
A titre d’exemple, imaginons qu’on fait un sondage sur une population et qu’on demande leur salaire mensuelle. On pourra remarquer que plus le montant du salaire augmente, plus cette information est absente. On peut supposer que les gens les plus fortunés ne souhaitent pas divulguer le montant de leurs revenus.
Les données NMAR sont les plus délicates à traiter car l’absence d’une donnée est motivée par une cause que nous avons interêt à comprendre pour mieux traiter ces données absentes. On dit qu’il s’agit d’un pattern d’absence de données non ignorable.
Pourquoi tout ce charabia ?
Quand une hypothèse MCAR ou MAR est remplie, on dit que le pattern d’absence de données est ignorable. En d’autre mots, il n’y a pas besoin de modéliser le comportement régissant l’absence de données pour une feature X car il est aléatoire.
Par ailleurs, quand les données ne sont ni MCAR ni MAR on dit que le pattern d’absence de données n’est pas ignorable. Ainsi, il faut modéliser le comportement d’absence de données pour mieux traiter ces données manquantes. Par ailleurs, modéliser un comportement d’absence de données requiert une compréhension profonde du sens métier des données qu’on manipule.
En réalité, savoir le pattern d’absence de données se fait avant tout par hypothèse. Il n’existe pas de règle universelle pour dire si une donnée manquante est une MCAR, MAR ou NMAR. Il est toujours important d’observer et comprendre le jeu de données pour décider quelle approche à utiliser pour traiter ces données manquantes.
Méthodes pour traiter les données manquantes
Traiter les données manquantes revient à « réparer » le jeu de données pour qu’il puisse être utilisable par les algorithmes de Machine Learning. La réparation d’un jeu de données peut prendre plusieurs formes : Comme supprimer les donner manquantes ou les remplacer les valeurs manquantes par des valeurs artificielles (on parle d’imputation).
A noter que ces techniques ne sont pas des astuces magiques pour répondre à tous les besoin. Réparer un jeu de données a des répercussions sur ce dernier. Notamment la perte d’informations et de consistance du jeu de données.
Suppression des observations (Complete case Analysis)
Il s’agit de la technique la plus simple et courante. Elle consiste à supprimer les observations (les lignes) qui contiennent au moins une feature manquante. Le jeu de données résultat ne contiendra aucune observation comportant une valeur manquante. C’est le comportement par défaut dans plusieurs outils statistiques.
Le problème de cette technique est qu’on peut être amené à supprimer un grand nombre d’observations. En effet, imaginons qu’on manipule un jeu de données de 1000 observations, et chaque observation est définie par 20 caractéristiques (features). Si chaque feature de notre jeu de données comporte 5% de valeurs manquantes, on devra supprimer 640 observations pour que notre jeu de données ne contiennent aucune valeur manquante. Ainsi notre jeu de données après traitement avec cette méthode ne comportera que 360 observations !
La limitation de cette solution est qu’on peut facilement écarter beaucoup d’observations. Or, ce sont des fragments d’informations qui seront perdus et qui ne pourront être exploités lors de la phase d’apprentissage des algorithmes de Machine Learning. Par conséquent, le modèle produit suite à la phase d’apprentissage risque de ne pas être performant.
Imputation de données
L’imputation de données manquante réfère au fait qu’on remplace les valeurs manquantes dans le jeu de données par des valeurs artificielles. Idéalement, ces remplacements ne doivent pas conduire à une altération sensible de la distribution et la composition du jeu de données.
Imputation par règle
Si on connait le sens métier de la donnée manquante et la règle métier la régissant, on peut faire une imputation par règle. Il s’agit tout simplement d’appliquer un algorithme définissant les règles métier pour mettre telle ou telle valeur en fonction des paramètres de l’algorithme.
Par exemple, si on a une variable âge et une autre représentant le fait qu’un individu soit majeur ou non (valeur vrai ou faux), on peut appliquer un algorithme qui remplira la variable majeur par vrai ou faux en fonction de l’âge (si l’âge est plus grand que 18 alors il/elle est majeur(e) sinon on mets faux).
Imputation par moyenne ou mode
Une autre façon intuitive d’imputer les valeurs manquantes d’une feature numérique est d’utiliser par la moyenne des observations. Pour les données qualitatives, on peut remplacer les valeurs manquantes de chaque feature par le mode de cette variable explicative.
Toutefois, l’imputation par moyenne est sujette à des limitations et il faut l’utiliser avec précaution. En effet, cette méthode peut sensiblement modifier le jeu de données. Ceci est principalement à cause de la moyenne qui est très sensible aux valeurs aberrantes.
Imputation par régression
Supposons qu’on estime un modèle de régression avec plusieurs variables explicatives. L’une d’entre elles, la variable X, comporte des valeurs manquantes. Dans ce cas on peut selectionner les autres variables explicatives (autre que X) et calculer un modèle prédictif avec comme variable à prédire X. Ensuite on applique ce modèle pour estime les différentes valeurs manquantes de X.
Concernant l’algorithme prédictif à utiliser, il n y a pas de règles strictes. On peut utiliser une régression logistique, régression numérique, l’algorithme Random Forest, ou tout autre. Du moment que les valeurs artificielles calculées soient proche du jeu de données.
La méthode Hot Deck
Traiter une valeur manquante d’une feature avec l’imputation Hot Deck revient à choisir aléatoirement une valeur parmi les valeurs de la même feature pour les autres observations du jeu de données. la valeur tirée au hasard est utilisée pour remplacer la valeur manquante.
Conclusion
Quelle que soit la technique de traitement des données manquantes, elles ne sauront remplacer un jeu de données complet et consistant. La réparation des données manquantes permet de « limiter la casse » tout en préservant au mieux la composition du jeu de données. Toutefois, peu importe le soin et la technique que nous employons pour traiter les données manquantes, il y aura toujours une perte d’informations contenus dans notre jeu de données et nous pourrons même introduire, à notre insu des biais qui ne reflètent pas nécessairement les relations régissant les données de notre data set.
Pour palier à ces problèmes, il est important d’essayer plusieurs techniques de traitement des données manquantes et voir celle qui fonctionne bien avec notre jeu de données.

Le traitement de la donnée manquante.. Ahhh!!! Que de belles expériences!
Pour moi, cela a constitué les parties les plus intéressantes dans les projets d’analyse de données. C’est l’occasion de développer des algorithmes sortis de presque nulle part. Les méthodes basées sur le Hot Deck sont les plus acceptées par les clients, puisque rien n’est inventé. On pige dans un jeu de valeurs réelles, le mot approximation fait si souvent peur (dans certains cas, à juste titre en effet)
C’est également une partie des plus chiantes pour beaucoup, et n’hésitent pas à user et abuser de la première méthode décrite, la suppression des observations. Mais quand le client a payé souvent cher la collecte de données (ex des enquêtes..) il est inconcevable d’en mettre une partie à la poubelle, faut faire avec. 🙂
Bonjour David !
Merci pour le partage de votre expérience. 🙂
Il est vrai que les projets de Data Science et surtout de traitement de données ont un gout d' »exploration » qui est difficilement maîtrisable. Cela va souvent à l’encontre de l’organisation des entreprises et la budgétisation de projets. Les méthodes Agiles permettent de remédier (partiellement) à cet effet.
Votre remarque sur la collecte de données est très pertinente ! En effet, dans l’air du Big Data, la donnée se veut peu chère (car à l’état brut), mais sa qualification et son traitement pour l’injecter dans un modèle prédictif la rend plus cher. Par contre, les données qui sont déja à la disposition des entreprises (données CRM, base de données…) restent assez propres et sont souvent prêtes à l’emploi.
Il faut surtout arrêter d’utiliser toutes les méthodes (anciennes) décrites ci-dessus car selon le statisticien Rubin elles sont « séduisantes mais dangereuses ». La seule façon de traiter honnêtement les données manquantes MAR est d’utiliser la technique robuste de l’imputation multiple. C’est une méthode qui provient de la statistique bayésienne et qui permet de prendre en compte l’incertitude que l’on porte sur ces observations manquantes.
Bonjour Adrien,
Rubin explique que les méthodes d’imputation au sens large (peu importe le procédé : hot deck / imputation par règle…etc) sont « séduisantes et dangereuses », principalement du fait qu’elles donne une confiance illusoire vis à vis de la pertinence des données imputées. Il estime que l’imputation est dangereuse car elle peut conduire à des remplacement des valeurs manquantes par d’autres mais qui échouent à capturer le phénomène que représente le jeu de données.
Finalement, la meilleure solution à apporter aux données manquantes est de ne pas en avoir! l’imputation des données est juste pour « approximer au mieux » les données que représente un phénomène qu’on ne maîtrise pas forcément.
Pour que l’information soit utile à tout le monde, je mets en bas un extrait du bouquin auquel vous faites référence.
https://books.google.fr/books?id=UUJ8mXgxOZUC&pg=PA188&lpg=PA188&dq=rubin+seducing+but+dangerous+MAR&source=bl&ots=95Uu5SgFXd&sig=ACIuxfQr6DycGmyhs21NJecvduU&hl=fr&sa=X&ved=2ahUKEwiimY-GtdvdAhUDCRoKHQqOBlEQ6AEwCHoECAgQAQ#v=onepage&q=rubin%20seducing%20but%20dangerous%20MAR&f=false
Très beau article sur les données manquantes, surtout ta conclusion cependant j’ai quelque question.
1) Que signifie l’expression « Les différents patterns d’absence de données » surtout le sens que tu donnes au mot patterns dans cette expression.
2) Quelques coquilles( en majuscule après avoir rappelé la section) après une lecture très succincte, donc pas forcement exhaustives
2-a)
Not Missing At Random (NMAR)
la probabilité… d’une valeur.
A titre d’exemple, … leur salaire mensuelle (MENSUEL).
2-b)
Méthodes pour traiter les données manquantes
Traiter … Learning. La réparation d’un jeu de données peut prendre plusieurs formes : Comme supprimer les donner(DONNEES) manquantes ou les remplacer les valeurs manquantes par des valeurs artificielles (on parle d’imputation).
Ping : MLOps: le secret pour un projet de machine learning réussi | by Félix Dumont | neoxia | Sep, 2023 - Cash AI