Lors de cet article, on découvrira l’algorithme K Nearest Neighbors (K-NN). Il s’agit d’un algorithme d’apprentissage supervisé. Il sert aussi bien pour la classification que la régression. Ainsi, nous allons voir le fonctionnement de cet algorithme, ses caractéristiques et comment il parvient à établir des prédictions.
C’est parti !

Découverte de l’algorithme K Nearest Neighbors
l’algorithme K-NN (K-nearest neighbors) est une méthode d’apprentissage supervisé. Il peut être utilisé aussi bien pour la régression que pour la classification. Son fonctionnement peut être assimilé à l’analogie suivante “dis moi qui sont tes voisins, je te dirais qui tu es…”.
Pour effectuer une prédiction, l’algorithme K-NN ne va pas calculer un modèle prédictif à partir d’un Training Set comme c’est le cas pour la régression logistique ou la régression linéaire. En effet, K-NN n’a pas besoin de construire un modèle prédictif. Ainsi, pour K-NN il n’existe pas de phase d’apprentissage proprement dite. C’est pour cela qu’on le catégorise parfois dans le Lazy Learning. Pour pouvoir effectuer une prédiction, K-NN se base sur le jeu de données pour produire un résultat.
Principe de K-NN : dis moi qui sont tes voisins, je te dirais qui tu es !
Comment K-NN effectue une prédiction ?
Pour effectuer une prédiction, l’algorithme K-NN va se baser sur le jeu de données en entier. En effet, pour une observation, qui ne fait pas parti du jeu de données, qu’on souhaite prédire, l’algorithme va chercher les K instances du jeu de données les plus proches de notre observation. Ensuite pour ces ![]() voisins, l’algorithme se basera sur leurs variables de sortie (output variable)
voisins, l’algorithme se basera sur leurs variables de sortie (output variable) ![]() pour calculer la valeur de la variable
pour calculer la valeur de la variable ![]() de l’observation qu’on souhaite prédire.
de l’observation qu’on souhaite prédire.
Par ailleurs :
- Si K-NN est utilisé pour la régression, c’est la moyenne (ou la médiane) des variables
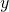 des
des 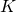 plus proches observations qui servira pour la prédiction
plus proches observations qui servira pour la prédiction - Si K-NN est utilisé pour la classification, c’est le mode des variables
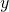 des
des 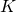 plus proches observations qui servira pour la prédiction
plus proches observations qui servira pour la prédiction
Ecriture algorithmique
On peut schématiser le fonctionnement de K-NN en l’écrivant en pseudo-code suivant :
Début Algorithme
Données en entrée :
- un ensemble de données
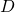 .
. - une fonction de définition distance
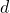 .
. - Un nombre entier
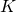
Pour une nouvelle observation ![]() dont on veut prédire sa variable de sortie
dont on veut prédire sa variable de sortie ![]() Faire :
Faire :
- Calculer toutes les distances de cette observation
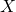 avec les autres observations du jeu de données
avec les autres observations du jeu de données 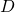
- Retenir les
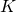 observations du jeu de données
observations du jeu de données 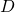 les proches de
les proches de 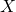 en utilisation le fonction de calcul de distance
en utilisation le fonction de calcul de distance 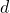
- Prendre les valeurs de
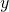 des
des 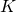 observations retenues :
observations retenues :
- Si on effectue une régression, calculer la moyenne (ou la médiane) de
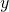 retenues
retenues - Si on effectue une classification , calculer le mode de
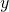 retenues
retenues
- Si on effectue une régression, calculer la moyenne (ou la médiane) de
- Retourner la valeur calculée dans l’étape 3 comme étant la valeur qui a été prédite par K-NN pour l’observation
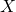 .
.
Fin Algorithme
Calcul de similarité dans l’algorithme K-NN
Comme on vient de le voir dans notre écriture algorithme, K-NN a besoin d’une fonction de calcul de distance entre deux observations. Plus deux points sont proches l’un de l’autre, plus ils sont similaires et vice versa.
Il existe plusieurs fonctions de calcul de distance, notamment, la distance euclidienne, la distance de Manhattan, la distance de Minkowski, celle de Jaccard, la distance de Hamming…etc. On choisit la fonction de distance en fonction des types de données qu’on manipule. Ainsi pour les données quantitatives (exemple : poids, salaires, taille, montant de panier éléctronique etc…) et du même type, la distance euclidienne est un bon candidat. Quant à la distance de Manhattan, elle est une bonne mesure à utiliser quand les données (input variables) ne sont pas du même type (exemple :age, sexe, longueur, poids etc…).
Il est inutile de coder, soi-même ces distances, généralement, les librairies de Machine Learning comme Scikit Learn, effectue ces calculs en interne. Il suffit juste d’indiquer la mesure de distance qu’on souhaite utiliser.
Pour les curieux, voici les définitions mathématiques des distances qu’on vient d’évoquer.
La distance euclidienne:
- distance qui calcule la racine carrée de la somme des différences carrées entre les coordonnées de deux points :
![]()
Distance Manhattan :
- la distance de Manhattan: calcule la somme des valeurs absolues des différences entre les coordonnées de deux points :
![]()
Distance Hamming :
- la distance entre deux points données est la différence maximale entre leurs coordonnées sur une dimension.
![]()
avec
Notez bien qu’il existe d’autres distances selon le cas d’utilisation de l’algorithme, mais la distance euclidienne reste la plus utilisée.
Comment choisir la valeur K ?
Le choix de la valeur ![]() à utiliser pour effectuer une prédiction avec K-NN, varie en fonction du jeu de données. En règle générale, moins on utilisera de voisins (un nombre
à utiliser pour effectuer une prédiction avec K-NN, varie en fonction du jeu de données. En règle générale, moins on utilisera de voisins (un nombre ![]() petit) plus on sera sujette au sous apprentissage (underfitting). Par ailleurs, plus on utilise de voisins (un nombre K grand) plus, sera fiable dans notre prédiction. Toutefois, si on utilise
petit) plus on sera sujette au sous apprentissage (underfitting). Par ailleurs, plus on utilise de voisins (un nombre K grand) plus, sera fiable dans notre prédiction. Toutefois, si on utilise ![]() nombre de voisins avec
nombre de voisins avec ![]() et
et ![]() étant le nombre d’observations, on risque d’avoir du overfitting et par conséquent un modèle qui se généralise mal sur des observations qu’il n’a pas encore vu.
étant le nombre d’observations, on risque d’avoir du overfitting et par conséquent un modèle qui se généralise mal sur des observations qu’il n’a pas encore vu.
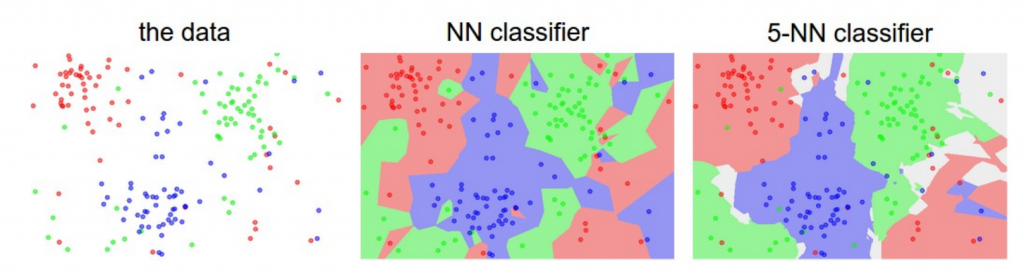
L’image ci-dessus à gauche représente des points dans un plan 2D avec trois types d’étiquetages possibles (rouge, vert, bleu). Pour le 5-NN classifieur, les limites entre chaque région sont assez lisses et régulières. Quant au N-NN Classifier, on remarque que les limites sont « chaotiques » et irrégulières. Cette dernière provient du fait que l’algorithme tente de faire rentrer tous les points bleus dans les régions bleues, les rouges avec les rouges etc… c’est un cas d’overfitting.
Pour cet exemple, on préférera le 5-NN classifier sur le NN-Classifier. Car le 5-NN classifier se généralise mieux que son opposant.
Limitations de K-NN
K-NN est un algorithme assez simple à appréhender. Principalement, grâce au fait qu’il n’a pas besoin de modèle pour pouvoir effectuer une prédiction. Le contre coût est qu’il doit garder en mémoire l’ensemble des observations pour pouvoir effectuer sa prédiction. Ainsi il faut faire attention à la taille du jeu d’entrainement.
Egalement, le choix de la méthode de calcul de la distance ainsi que le nombre de voisins ![]() peut ne pas être évident. Il faut essayer plusieurs combinaisons et faire du tuning de l’algorithme pour avoir un résultat satisfaisant.
peut ne pas être évident. Il faut essayer plusieurs combinaisons et faire du tuning de l’algorithme pour avoir un résultat satisfaisant.
Conclusion
Dans cet article, vous avez découvert l’algorithme K-NN. Vous avez appris également que :
- K-NN stocke tout le jeu de données pour effectuer une prédiction,
- K-NN ne calcule aucun modèle prédictif et il rentre dans le cadre du Lazy Learning,
- K-NN effectue des prédictions juste à temps (à la volée) en calculant la similarité entre un observation en entrée et les différentes observations du jeu de données,
J’espère que cet article vous a plu, si vous avez des questions n’hésitez pas à me les poser en commentaire. J’y répondrai du mieux que je peux. 🙂

Encore une explication de maître. vraiment très clair et une grande qualité…
aussi étant un grand curieux. je voudrai savoir l’onglet que vous avez utilisé sur votre éditeur pour avoir ce rendu dans la section:
« Principe de K-NN : dis moi qui sont tes voisins, je te dirais qui tu es ! ».
je construis un système en interne et je voudrai l’avoirpour les petit mémos.
MERCI
Merci Vakara pour votre commentaire fort sympa 😉
Bon courage
Merci pour l’explication c’est top.
Merci pour cet article intéressant, très informatif, et très bien expliqué.
Je lis pour la première fois la définition de K-NN, j’ai tout compris avant de finir ma tasse de café, chapeau bas.
Bonjour,
Savez si il est possible de fixer au distance maximum au de la de laquelle la données test s’éloigne trop des données d’entrainement et est donc considéré comme différente ? Ce qui permettrait en quelque sortes de trouver des « intrus » dans le jeu de données « test »
*une distance
Merci pour l’explication, j’ai tout compris.
Je vous suis reconnaissant pour cette explication, c’est excellent.
Bravo, explication de haute qualité!