Logistic regression (régression logistique) est un algorithme supervisé de classification, populaire en Machine Learning. Lors de cet article, nous allons détailler son fonctionnement pour la classification binaire et par la suite on verra sa généralisation sur la classification multi-classes.

La classification en Machine Learning

La classification est une tâche très répandue en Machine Learning. Dans ce genre de problématique, on cherche à mettre une étiquette (un label) sur une observation : une tumeur est-elle maligne ou non, une transaction est- elle frauduleuse ou non… ces deux cas sont des exemples de classification.

Quand on a deux choix d’étiquettes possibles (tumeur maligne ou non), on parle de Binary Classification (classification binaire). Par ailleurs, l’étiquette Y aura deux valeurs possibles 0 ou 1. En d’autres termes $Y \in \{0,1 \}$ .

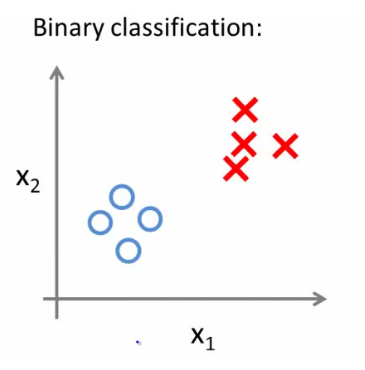
Le but du jeu c’est qu’on trouve une ligne (Boundary Decision) séparant les deux groupes (les cercles et les carrés).

Note : Pour l’exemple de la tumeur, on peut attribuer arbitrairement la classe (étiquette) 1 pour dire qu’il s’agit d’une tumeur maligne et la valeur 0 pour les tumeurs bénignes. On peut aussi faire l’inverse (dénoter 0 comme une tumeur maligne et 1 pour la bénigne), cela n’aura aucune incidence sur vos prédictions !

Quand notre problème a plusieurs étiquettes possibles (par exemple classifier un article dans une catégorie (« sport », « politique », « High-Tech »)…), on parle de Multi-class classification (Classification Multi classes). Dans ce cas, $Y \in \{ 1, 2, 3, ...\}$ . Encore une fois, on peut attribuer arbitrairement les numéros des classes aux observations du Training Set.

Sigmoid Function : La fonction pour la régression Logistique

Définition de la fonction Score

Logistic Regression est un modèle de classification linéaire qui est le pendant de la régression linéaire , quand $Y$ ne doit prendre que deux valeurs possibles (0 ou 1). Comme le modèle est linéaire, la fonction hypothèse pourra s’écrire comme suit :

$S(X^{(i)}) = \theta_{0} + \theta_{1} x_{1} + \theta_{2} x_{2} + \theta_{3} x_{3}+....+ \theta_{n} x_{n}$

avec :

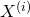$X^{(i)}$ : une observation (que ce soit du Training Set ou du Test Set), cette variable est un vecteur contenant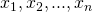 $x_{1}, x_{2},...,x_{n}$
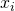$x_{i}$ : est une variable prédictive (feature) qui servira dans le calcul du modèle prédictif
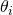$\theta_{i}$ : est un poids/paramètre de la fonction hypothèse. Ce sont ces 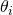$\theta_{i}$ qu’on cherche à calculer pour obtenir notre fonction de prédiction
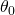$\theta_{0}$ est une constante nommée le bias (biais)

On peut observer qu’on peut réécrire $\theta_{0}$ en : $\theta_{0}$ $x_{0}$ avec $x_{0} = 1$ , Cela nous permet de réécrire notre fonction $S(X)$ de façon plus compacte comme suit :

$S(X)$ = $\sum_{i=0}^{n + 1} (\theta_{i} x_{i})$

On a définit précédemment $X^{(i)}$ comme étant un vecteur de $x_{1}, x_{2},...,x_{n}$ . Faisant la même chose pour les $\theta_{(i)}$ :

soit grand théta $\Theta$ le vecteur contenant $\theta_{0}, \theta_{1},..., \theta_{n},$ .

Notre fonction hypothèse peut- être vue comme le produit de deux vecteurs $\Theta$ et $X$ :

$S(X)$ = $\Theta$ $X$

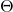
Note : Si vous ne connaissez pas le calcul vectoriel/matriciel nous vous en faites pas. Rappelez vous juste que cette représentation compacte est équivalente à celle qui ne l’est pas.

On appelle cette fonction hypothèse : la fonction score. L’idée est de trouver des coefficients $\theta_{0}$ , $\theta_{1}$ , …, $\theta_{n}$ de sorte que :

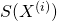
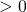$S(X^{(i)})$ $> 0$ quand la classe (étiquette) vaut 1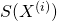
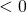$S(X^{(i)})$ $< 0$ quand la classe (étiquette) vaut 0

Sigmoid Function pour calculer la probabilité d’une classe

La fonction score qu’on a obtenue intègre les différentes variables prédictives (les $x_{i}$ ). A cette fonction, on appliquera la fonction sigmoid (Sigmoid Function). Cette fonction produit des valeurs comprises entre 0 et 1.

Le résultat obtenu par la fonction sigmoid est interprété comme la probabilité que l’observation X soit d’un label (étiquette) 1.

La fonction Logistique (autre nom pour la fonction Sigmoid), est définie comme suit

$Sigmoid(x) = \frac{1}{1 + e^{-x}}$

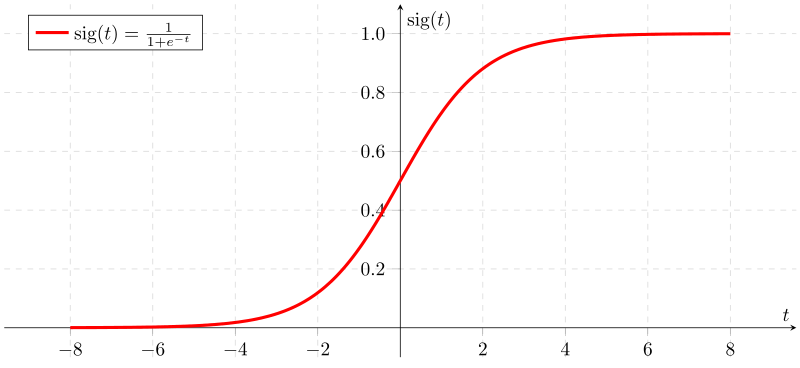
En analysant la courbe ci-dessus, On peut remarquer trois choses :

Elle passe par l’ordonnée 0.5 quand $x = 0$ : $Sigmoid (0) = 0.5$
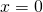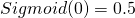
La fonction Sigmoid asymptote à 0 et 1 (elle s’approche des ordonnées 0 et 1 mais sans les « toucher »)
On remarque que 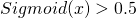$Sigmoid(x) > 0.5$ quand x > 0 et Sigmoid (x) < 0.5 quand x < 0

En appliquant cette fonction sigmoid sur notre fonction score, on obtient notre fonction hypothèse pour la régression logistique :

$H (X) = Sigmoid (S(X))$ = $Sigmoid (\Theta X)$

Ce qui donne :

$Sigmoid(\Theta X) = \frac{1}{1 + e^(\Theta X)}$

Interprétation des résultats

L’interprétation de la valeur calculée par la fonction sigmoid est simple :

Le nombre renvoyé par la fonction Sigmoid représente la probabilité que l’observation soit de la classe 1 (la classe positive)

Si on reprend l’exemple des tumeurs, si H(X) nous renvoie 0.7, cela veut dire que le patient à 70% de chances d’avoir une tumeur cancéreuse. En d’autres termes, il a 30% de chances d’avoir une tumeur bénigne.

Plus formellement, la probabilité que X soit de classe (étiquette/label) 1 avec les paramètres $\Theta$ :

$H(X)$ = $P(y = 1 | X; \Theta)$

On peut déduire facilement la probabilité que Y valuée à 0 comme suit :

$P(y = 0 | X; \Theta) = 1 - P(y = 1 | X; \Theta)$

Généralisation de la Logistic Regression à la classification multi classes

Telle qu’on l’a vu jusqu’ici, Logistic Regression permet uniquement de classifier binairement les observations (Spam/Non SPAM, MALIGNE/BENIGNE, NOIR/BLANC…) ce qui est assez contraignant !

Imaginez maintenant que vous ayez à classifier une observation dans une catégorie parmi trois. Par exemple, classer un article de presse dans une des trois catégories : Sport, High-Tech ou politique. Dans ce cas, on parle de Multi-class classification. L’étiquette Y $\in \{0, 1, 2 \}$ .

Note : On parle de Multiclass classification du moment que le nombre de labels (étiquettes) possible est supérieur à 2.

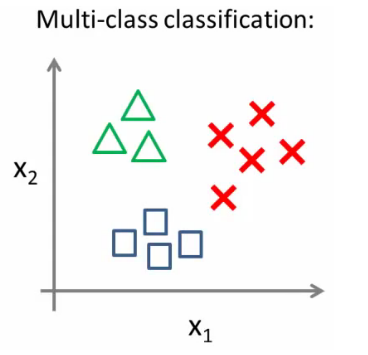
L’algorithme : One vs All

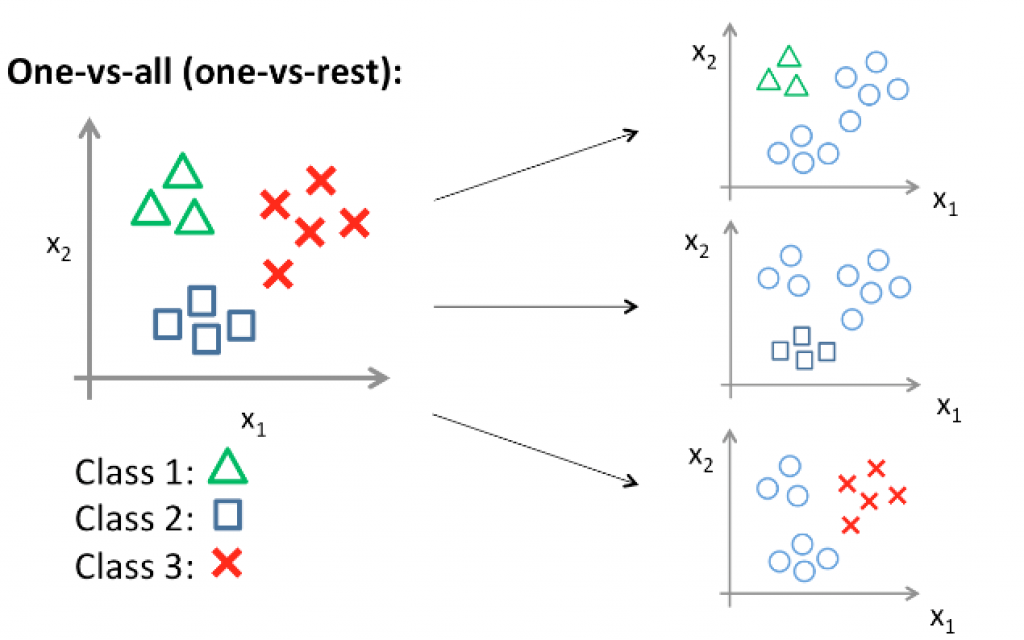
L’algorithme One-Versus-All (One vs All) permet d’utiliser Logistic Regression pour la classification multi-classes. Le principe est simple : Il consiste à découper le problème de classification multi-classes en une multitude de problèmes de classification binaires.

Supposant que le triangle vert correspond à la classe 1, le carré bleu à la classe 2 et la croix rouge à classe 3. L’algorithme One-vs All va procéder comme suit :

Etape 1 : On considère que les triangles sont la classe positive (étiquette 1) et le reste comme la classe négative (dans ce cas, les carrés et les croix seront dans le même groupe de classe négative (étiquette 0) ), et on entraîne la régression logistique sur cette configuration de données. Ce qui produira une fonction de prédiction $H^1(x)$
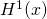
Etape 2 : On considère les carrés comme la classe positive et le reste comme la classe négative, et on entraîne la régression logistique pour obtenir une deuxième fonction de prédiction : $H^2(x)$
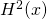
Etape 3 : On considère les croix comme la classe positive et le reste comme la classe négative, et on entraîne la régression logistique pour obtenir $H^3(x)$

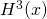
Chacune des ces fonctions de prédiction $H^1(x)$ , $H^2(x)$ , $H^3(x)$ nous donnera la probabilité que x soit de la classe $Y_{i}$ . La bonne classe de l’observation x est celle pour laquelle on a obtenu la plus grande probabilité.

En d’autres termes, la classe de x est le $\underset{i \in \{ 1,2, ...,K\}}{max H^i(x)}$ , avec $K$ le nombre de classes (étiquettes) possibles.

Résumé

Dans cet article, vous avez découvert le principe de fonctionnement de Logistic Regression. Il s’agit d’un algorithme de classification populaire. Vous connaissez maintenant :

Comment est définie la fonction score et comment on peut la réécrire de façon plus compacte
La réprésentation et l’intérêt de la fonction logistique (Sigmoid Function)
Comment généraliser la classification binaire de la régression logistique pour des problèmes multi-classes en utilisant one-vs-all algorithm.

J’ai fait le choix de ne pas parler dans ce billet du comment on calcule les coefficients $\theta_{0}, \theta_{1}...$ , mais je le ferai lors d’un prochain article. Si vous êtes curieux, il s’agit de la méthode maximum-likelihood estimation (méthode de vraisemblance maximale).

Finalement, pour la classification multi-classes, il existe une autre alternative au one-vs-all. Cette alternative est la fonction Softmax (on parle de Softmax Regression). La fonction Softmax permet de renvoyer d’un seul coup la probabilité d’appartenance à chaque classe. Si par exemple $Y \in \{ 0,1,2 \}$ , la fonction Softmax renverra un tableau contenant trois probabilité d’appartenance à la classe 0, 1 ou 2 respectivement. Softmax Regression fera l’objet d’un article futur.

Finalement, si des éléments dans cet article nous vous sont pas clairs ou si vous avez des questions, n’hésitez pas à me les poser par commentaire. J’y répondrai du mieux que je peux. 🙂

mongan agbeshie 16 avril 2019

Bonjour Younes

Ce pour quoi, j’ai visité ta page touche à sa fin et c’est très plaisant de lire vos articles ( j’ai en lu 8 et celui sur Softmax Regression par le biais du lien qui m’a ramené sur Wikipédia), j’ai appris beaucoup en 3 heures sur l’apprentissage automatique et J’ai kiffé grave sur la structure de tes articles.

Malheureusement , je ne suis certain d’avoir vu toutes les coquilles possibles vu le temps qui me fait défaut et j’invite chaque visiteur à apporter sa contribution, je remercie ceux qui avant moi ont commenté vos articles dans le sens de son amélioration.

Ce que j’ai appris de ton travail (et qui à mon humble avis reflète ta personnalité) c’est qu’il faut « diviser pour mieux expliquer », le fait de diviser les notions (concepts) en de petits articles est très efficace pour la compréhension.

Concernant cet article, j’ai 4 observations à faire:

1) Revoir la définition de la fonction score , à te lire tu as défini la fonction hypothèse alors qu’il s’agit bien du score sauf erreur de ma part.
autrement dit il faut remplacer dans cette définition le mot HYPOTHESE par le mot SCORE .
2) Dans la suite tu donnes l’impression que la fonction score est un cas particulier de la fonction hypothèse alors que tu as juste fait des hypothèses sur la fonction score, pourrais-tu m’éclairer la dessus et revoir cette partie si nécessaire.

3) Tu as bien défini le vecteur grand thêta, mais tu n’as pas défini le vecteur grand X (inspires-toi simplement de celle de grand thêta)

4) Dans l’écriture matricielle du score (S(X)=OX), partant de la norme (convention) qui consiste à dire que les vecteurs sont des vecteurs colonnes (sauf mention contraire) , il est plus juste d’écrire S(X)=Transposée (O)X.

NB: je m’excuse des probables fautes dans mes commentaires

Répondre ↓

11 réflexions au sujet de « Logistic Regression pour Machine Learning – Une Introduction Simple »

FALFLOUI HAITAM 22 juin 2018

Merci Mr younes vraiment une introduction très simple est claire pour la régression logistique.

Répondre ↓
1. Younes Benzaki Auteur de l’article22 juin 2018
  
  Merci Haitam pour le commentaire 😉
  
  Répondre ↓
mongan agbeshie 16 avril 2019

Bonjour Younes

Ce pour quoi, j’ai visité ta page touche à sa fin et c’est très plaisant de lire vos articles ( j’ai en lu 8 et celui sur Softmax Regression par le biais du lien qui m’a ramené sur Wikipédia), j’ai appris beaucoup en 3 heures sur l’apprentissage automatique et J’ai kiffé grave sur la structure de tes articles.

Malheureusement , je ne suis certain d’avoir vu toutes les coquilles possibles vu le temps qui me fait défaut et j’invite chaque visiteur à apporter sa contribution, je remercie ceux qui avant moi ont commenté vos articles dans le sens de son amélioration.

Ce que j’ai appris de ton travail (et qui à mon humble avis reflète ta personnalité) c’est qu’il faut « diviser pour mieux expliquer », le fait de diviser les notions (concepts) en de petits articles est très efficace pour la compréhension.

Concernant cet article, j’ai 4 observations à faire:

1) Revoir la définition de la fonction score , à te lire tu as défini la fonction hypothèse alors qu’il s’agit bien du score sauf erreur de ma part.
autrement dit il faut remplacer dans cette définition le mot HYPOTHESE par le mot SCORE .
2) Dans la suite tu donnes l’impression que la fonction score est un cas particulier de la fonction hypothèse alors que tu as juste fait des hypothèses sur la fonction score, pourrais-tu m’éclairer la dessus et revoir cette partie si nécessaire.

3) Tu as bien défini le vecteur grand thêta, mais tu n’as pas défini le vecteur grand X (inspires-toi simplement de celle de grand thêta)

4) Dans l’écriture matricielle du score (S(X)=OX), partant de la norme (convention) qui consiste à dire que les vecteurs sont des vecteurs colonnes (sauf mention contraire) , il est plus juste d’écrire S(X)=Transposée (O)X.

NB: je m’excuse des probables fautes dans mes commentaires

Répondre ↓
Diallo 6 mai 2019

Merci beaucoup, j’ai réellement compris le sens de la régression logistique grâce à cette introduction.

Répondre ↓
1. Younes Benzaki Auteur de l’article15 mai 2019
  
  avec plaisir Diallo 🙂
  
  Répondre ↓
alex 15 août 2019

Petite erreur, la fonction sigmanoïde dans le texte comporte une erreur au dénominateur (« -« x) cependant que le graphique c est correct.

Répondre ↓
1. Younes Benzaki Auteur de l’article25 août 2020
  
  Effectivement, c’est corrigé !
  
  Merci
  
  Répondre ↓
Amine 6 février 2020

Merci Youness, c’était bien claire et simple à comprendre
J’ai une question stp, quand pourra t’on choisir cet algorithme comme modèle de prédiction, quels sont les critères qu’on peut prendre en compte ?
Merci d’avance, 🙂

Répondre ↓
1. Younes Benzaki Auteur de l’article24 août 2020
  
  Bonjour Amine,
  
  Tout dépend de la situation que vous avez entre les mains. S’il s’agit d’un petit jeu de données assez simple avec une classification binaire, la régression logistique suffit. Pour des cas plus complexes, le mieux est d’entrainer plusieurs algorithmes de classification (notamment SVM, Random Forest…etc) et d’en garder celui ou ceux qui produisent les meilleurs résultats.
  
  Bien à vous
  Younes
  
  Répondre ↓
Mohamed Hassene 12 juin 2020

very well explained, thank you very much.

Répondre ↓
1. Younes Benzaki Auteur de l’article24 août 2020
  
  Thank you too for reading the blog post 🙂
  
  Répondre ↓

Laisser un commentaire Annuler la réponse

Ce site utilise Akismet pour réduire les indésirables. En savoir plus sur comment les données de vos commentaires sont utilisées.