Naive Bayes Classifier est un algorithme populaire en Machine Learning. C’est un algorithme du Supervised Learning utilisé pour la classification. Il est particulièrement utile pour les problématiques de classification de texte. Un exemple d’utilisation du Naive Bayes est celui du filtre anti-spam.

Regardons de plus prés comment fonctionne cet algorithme.

Probabilités conditionnelles

Le naive Bayes classifier se base sur le théorème de Bayes. Ce dernier est un classique de la théorie des probabilités. Ce théorème est fondé sur les probabilités conditionnelles.

Probabilités conditionnelles : Quelle est la probabilité qu’un événement se produise sachant qu’un autre événement s’est déjà produit.

Exemple :

Supposons qu’on ait une classe de lycéens. Soit et les deux événements suivants :

• l’événement 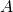: l’élève est une fille.
• L’événement 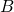: l’élève pratique l’allemand.

Quelle est la probabilité qu’on choisisse au hasard une fille pratiquant l’allemand ?

Le théorème de Bayes permet de calculer ce genre de probabilité.

Notons la probabilité d’un événement.

Cela équivaut à calculer

Le terme se lit : la probabilité que l’événement A se réalise sachant que l’événement B s’est déjà réalisé.

On appelle le terme A : l’évidence (faux ami avec le mot anglais Evidence). Le terme B s’appelle Outcome.

Théorème de Bayes

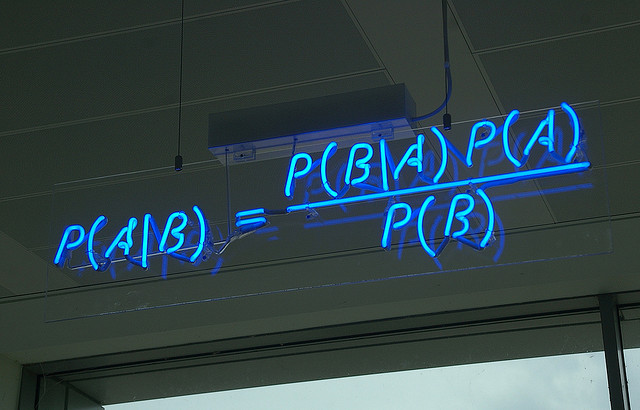
Formule du théorème de Bayes

Reprenons l’exemple des lycéens pratiquant l’allemand. Imaginons le jeu de données suivant :

	Fille ()	Garçon ()	Totaux
Allemand ()	10	7	17
Autre langue ()	4	9	13
Totaux	14	16	30

Calculons la probabilité suivante : Quelle est la probabilité qu’on tire au hasard un élève parlant Allemand sachant qu’elle est une fille ?

Selon la formule de Bayes on a :

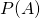• est la probabilité de prendre au hasard une fille de la population des élèves de la classe. On appelle 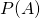la probabilité antérieure (prior probability).

Ce qui donne :

Note:

• le cardinal d’un ensemble est le nombre d’éléments dans ce dernier
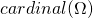• représente l’ensemble des lycéens de notre exemple (l’univers de probabilités)

Naive Bayes Classifier

Lors de l’exemple précédent, nous avons appliqué le théorème de Bayes avec une seule variable prédictive (Evidence) : A savoir le sexe de l’élève. Dans les vraies applications du Naive Bayes, on calcule le résultat (Outcome) en se basant sur plusieurs variables. L’application du théorème de Bayes sur plusieurs variables rend le calcul complexe. Pour contourner cela, une approche consiste à prendre en considération ces variables indépendamment les unes des autres. Il s’agit d’une hypothèse forte. Généralement, les variables prédictives sont liées entre elles. Le terme « naïve » vient du fait qu’on suppose cette indépendance des variables.

Naïve Bayes est particulièrement prisé dans les problèmes de classification de texte

Si on prend l’exemple de classification de mails en , Naïve Bayes se basera sur la fréquence d’occurrence des mots dans le mail pour en définir la catégorie. Lors de sa classification, l’algorithme supposera que les mots du mail « apparaissent » indépendamment les uns des autres. Évidemment, d’un point de vue linguistique et sémantique, cette supposition est fausse !

Classification multi-classes avec Naive Bayes

Pour mieux comprendre le Naive Bayes Classifier, déroulons le sur un exemple simple.

Note : l’exemple ci-dessus est inspiré d’une discussion sur le site StackOverflow.

Supposons qu’on ait un jeu de données sur 1000 fruits. On dispose de trois types : Banane, Orange, et « autre ». Pour chaque fruit, on a 3 caractéristiques :

• Si le fruit est long ou non
• S’il est est sucré ou non
• Si sa couleur est jaune ou non

Notre jeu de données se présente comme suit :

Type	Long	petit ( long)	sucré	sucré	Jaune	Pas jaune	Total
Banane	400	100	350	150	450	50	500
Orange	0	300	150	150	300	0	300
Autre fruit	100	100	150	50	50	150	200
Total	500	500	650	350	800	200	1000

Note:

• le symbole signifie la négation ( froid chaud)

L’idée du jeu est de prédire le type d’un fruit (orange, banane ou autre) qu’on n’a pas encore vu. Ceci en se basant sur ses caractéristiques.

Supposons que quelqu’un nous demande de lui donner le type d’un fruit qu’il a. Ses caractéristiques sont les suivantes :

• Il est jaune
• Il est long
• Il est sucré

Pour savoir s’il s’agit d’une banane, ou d’une orange ou d’un autre fruit, il faut qu’on calcule les trois probabilités suivantes:

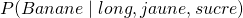• : La probabilité qu’il s’agisse d’une banane sachant que le fruit est long, jaune et sucré
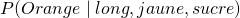• : La probabilité qu’il s’agisse d’une orange sachant que le fruit est long, jaune et sucré
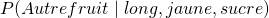• : La probabilité qu’il s’agisse d’un autre fruit sachant que ce dernier est  long, jaune et sucré

Le type du fruit « inconnu » qu’on cherche à classifier sera celui où on a la plus grande probabilité.

Selon la formule de Bayes, on a :

• =

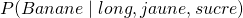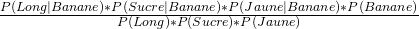
Avec notre jeu de données, on peut calculer facilement un certain nombre de probabilités :

De même :

• 
• 
• 
• 
• 

Calculons maintenant le terme : : Probabilité que le fruit est long sachant qu’il s’agit d’une banane.

Avec la même logique, on peut calculer les probabilités suivantes : et . Je vous invite à les calculer comme guise d’entraînement. 😉

Maintenant, qu’on a toutes nos probabilités utiles pour notre calcul, on peut calculer la probabilité suivante :

Avec la même logique on obtient :

 

On remarque que la probabilité que notre fruit soit une banane est largement plus grande que celle des autres probabilités. On classifie notre fruit inconnu comme étant une banane.

 

Avantages et limitations du Naive Bayes Classifier ?

Avantages

En se basant sur l’exemple de classification des fruits, on remarque plusieurs avantages pour cet algorithme :

• le Naive Bayes Classifier est très rapide pour la classification : en effet les calculs de probabilités ne sont pas très coûteux.
• La classification est possible même avec un petit jeu de données

Inconvénients

• l’algorithme Naive Bayes Classifier suppose l’indépendance des variables : C’est une hypothèse forte et qui est violée dans la majorité des cas réels.

Contre intuitivement, malgré la violation de la contrainte d’indépendance des variables, Naïve Bayes donne de bons résultats de classification. La publication de Harry Zhang donne une explication sur cette performance contre intuitive (Le publication est assez technique 🙂 ).

 

Vous connaissez maintenant le fonctionnement en coulisse du Naive Bayes Classifier. Si vous avez des questions sur son fonctionnement n’hésitez pas à les poster en commentaire. Et si l’article vous plait, n’oubliez pas de le faire partager ! 🙂