Vous avez 10 minutes de temps libre pour comprendre la régression polynomiale (Polynomial Regression) pour faire des prédictions ? Cet article est fait pour vous ! c’est parti ! 🙂

Après l’article sur la régression linéaire univariée et la régression linéaire multivariée, on va maintenant attaquer la régression polynomiale. Cette dernière est tout simplement une généralisation de la régression linéaire multivariée.

L’intérêt de la régression polynomiale est de pouvoir introduire de la non-linéarité dans l’analyse prédictive. La régression polynomiale permet de trouver une fonction de prédiction adéquate pour des données qui ne semblent pas avoir une relation linéaire.

Qui dit polynomiale dit Polynôme !

Il n’est pas question de faire un cours d’algèbre dans cet article, mais retournons aux bancs de l’école pour quelques minutes pour revoir ce que c’est un polynôme.. 😉

Qu’est ce qu’un monôme ?

Un monôme est une expression de la forme : $\alpha x\textsuperscript{n}$ .

Avec :

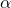$\alpha$ : un nombre réel (ou complexe) appelé le coefficient du monôme.
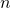$n$ un entier naturel : représentant le degré du monôme.

Exemple :

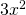$3x\textsuperscript{2}$ est un monôme du second degré et de coefficient 3
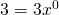$3 = 3x\textsuperscript{0}$ est un monôme de degré 0 et de coefficient 3

Qu’est ce qu’un polynôme ?

Un polynôme est tout simplement la somme de plusieurs monômes. Le degré d’un polynôme est la puissance la plus élevée de ses monômes.

Exemple :

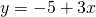$y = -5 + 3x$ est un polynôme de degré 1
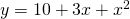$y = 10 + 3x +x\textsuperscript{2}$ est un polynôme de degré 2

Graphiquement, à quoi ressemble un polynôme ?

Regardons à quoi ressemble un graphiquement le polynôme de premier degré : $-10 + 3x$ :

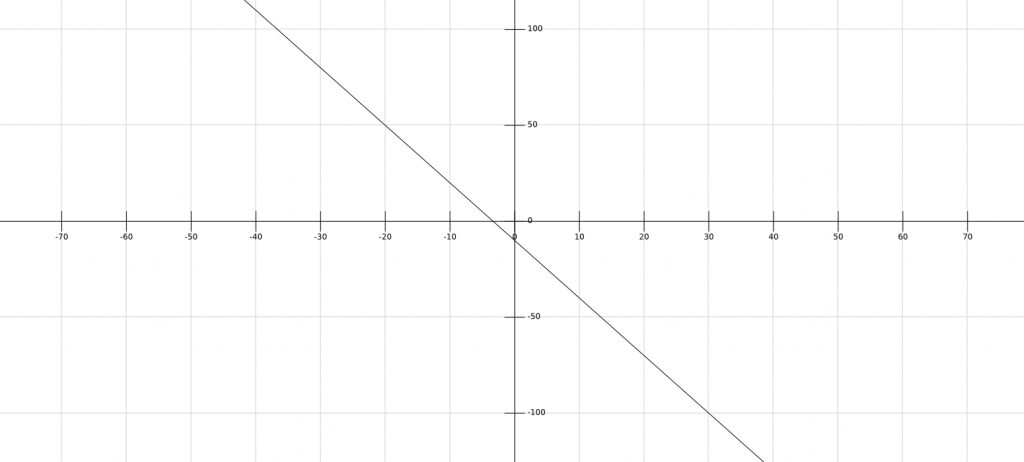
first degree polynomial

$y = -10 - 3x$

Regardons maintenant la courbe d’un polynôme de second degré

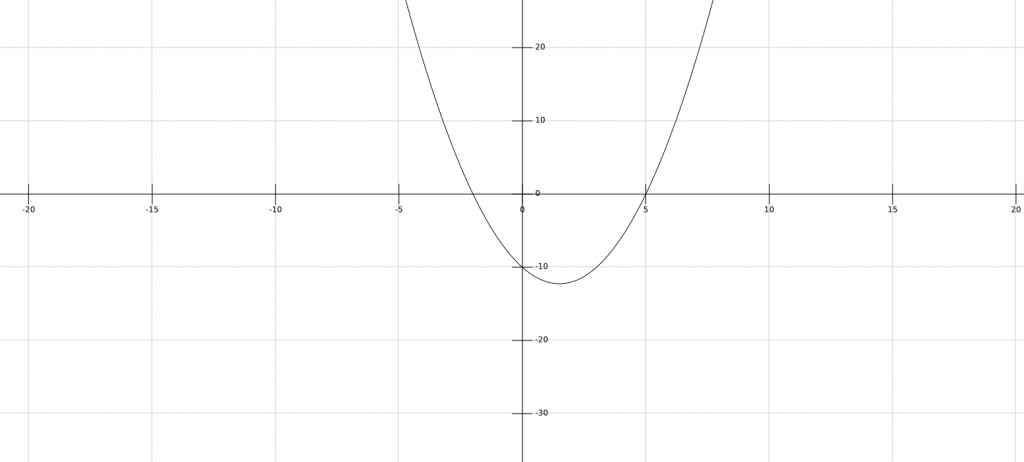
second degree polynomial

$y = -10 - 3x + x\textsuperscript{2}$

Et pour finir, la courbe d’un polynôme de 3ème degré

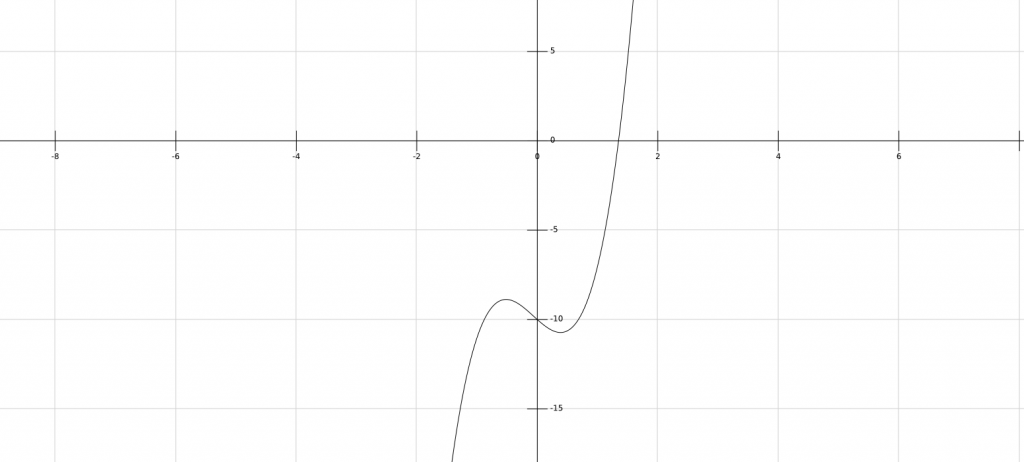
third degree polynomial

$y = -10 -3x + x\textsuperscript{2} + 5x\textsuperscript{3}$

Intuitivement, chaque nouvel ordre du polynôme va rajouter un « pli » à la courbe.

Polynomial Regression : une fonction de prédiction sous forme de polynôme ?

Dans mon article sur la régression linéaire multivariée, on a vu que la fonction de prédiction s’écrivait comme suit :

$F(X) = \epsilon + \alpha x_1 + \beta x_2 + \gamma x_3+...+ \omega x_n}$

Bien que plusieurs variables prédictives entraient en jeu ( $x_1,x_2,...$ ), la fonction de prédiction reste un polynôme de premier degré.

En régression polynomiale, on évalue chaque variable prédictive en l’associant à tous les degrés polynomiaux de $1$ à $k$ .

Par exemple, si on a deux variables prédictives $x_1$ et $x_2$ , un modèle polynomial de second degré s’écrira ainsi :

$F(X) = \epsilon + \alpha x_1 + \beta x_2 + \gamma x_1\textsuperscript{2} + \lambda x_2\textsuperscript{2}}$

A noter que :

- $\epsilon$ : est une constante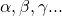
- $\alpha, \beta, \gamma...$ : représente les coefficients de notre fonction prédictive F(X)
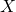- $X$ : est un vecteur/tableau de variables prédictives (lire cet article sur la représentation des données)
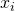- $x_i$ : représente la 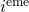$i\textsuperscript{eme}$ variable prédictive

Parlons Python !

Trêve de bavardage, parlons du concret ! On utilisera la régression polynomiale pour trouver un modèle prédictif.

Supposons, qu’un site e-commerce souhaite savoir si le temps de chargement des pages web de son site impacte le montant du panier moyen de l’internaute.

On souhaite trouver une fonction de prédiction qui modélisera cette corrélation.

Note : Ne disposant pas d’un vrai jeu de données, j’en créerai un, aléatoire, pour illustrer la régression polynomiale.

Création d’un jeu de données


import numpy as np
import matplotlib.pyplot as plt
#initialisation du générateur 
np.random.seed(2)
# génération de 1000 nombres aléatoires distribués selon la loi normale X ~ N(3, 1) 
#en d'autre terme, les pages chargeront en moyenne en 3 secondes et un ecart-type de 1 seconde. 
tempsChargementPages = np.random.normal(3.0, 1.0, 1000)
génération aléatoires de montants d'achat corrélés aux temps de chargement
montantAchat = np.random.normal(50.0, 10.0, 1000) / (tempsChargementPages * tempsChargementPages)
# le temps de chargement de la page est notre variable prédictive
x = np.array(tempsChargementPages)
# montantAchat est la variable cible (qu'on cherche à prédire)
y = np.array(montantAchat)

Visualisation des données

Regardons à quoi ressemble visuellement notre jeu de données factice.


axes = plt.axes()
axes.grid()
plt.xlabel('temps de chargement en secondes')
plt.ylabel('montant des achats euros')
plt.scatter(tempsChargementPages, montantAchat)
plt.show()

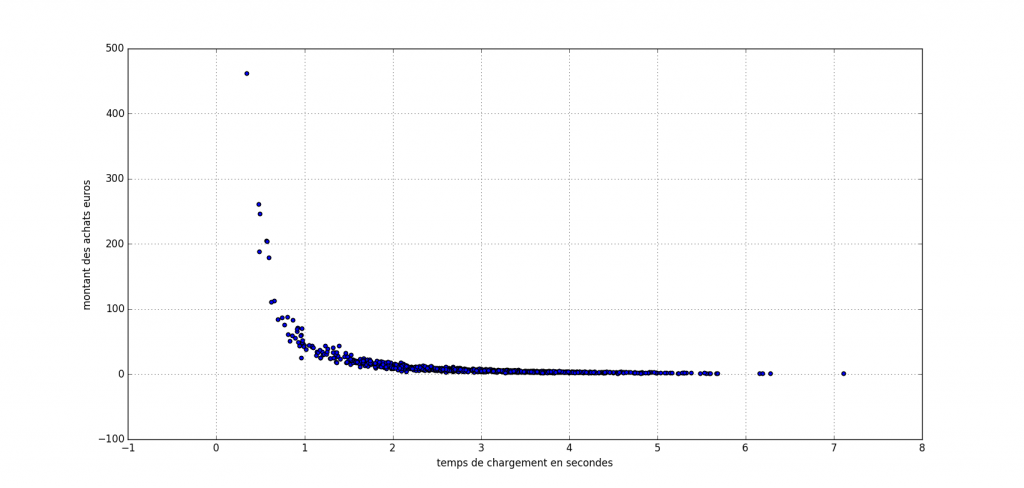
polynomial regression dataset visualisation

On voit clairement que la corrélation entre le prix du panier et le temps de chargement des pages du site n’est pas linéaire. Par ailleurs, moins la page met du temps à charger, plus le prix du panier moyen augmente.

Retrouver une fonction polynomiale

Python offre via sa librairie numPy une fonction polyfit qui permet de construire un modèle polynomial de degré $n$ qui convient bien à nos données (en minimisant au maximum la marge d’erreur).

Rappelons nous que plus on rajoute un degré au polynôme, plus ce dernier devient sensible aux données et s’y adapte mieux.

Essayons de trouver un modèle avec un polynôme de 4 degrés.


p4 = np.poly1d(np.polyfit(x, y, 4))
#print p4
xp = np.linspace(0, 7, 100)
plt.plot(xp, p4(xp), c='r')

Le polynôme que nous retrouve python est le suivant :

$F(X) = 1.71 x\textsuperscript{4} - 27.23x\textsuperscript{3} + 153.3 x\textsuperscript{2} - 362.8 x + 310.6$

Note : Si vous refaites ce tutoriel chez vous, il se peut que vous ayez des coefficients différents. Cela est dû au caractère aléatoire des nombres générés de notre jeu de données.

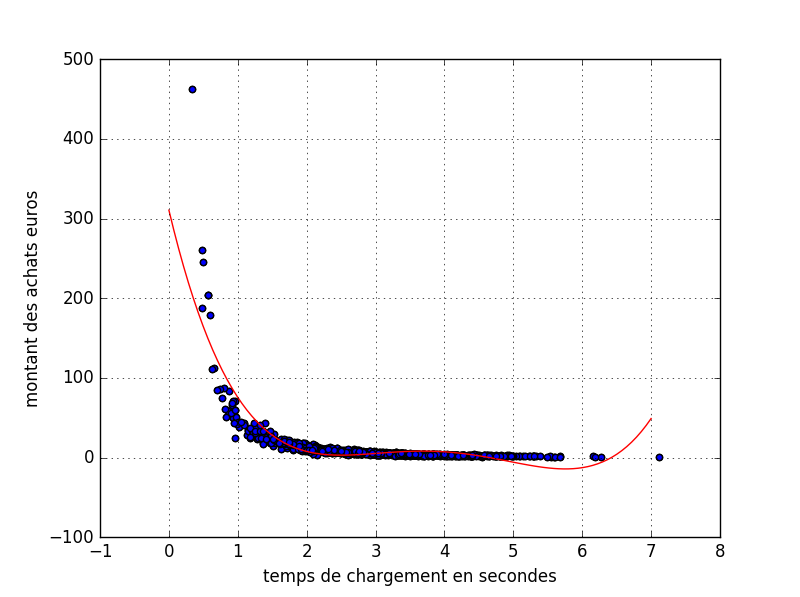
polynomial regression fitting model

Et voila ! notre fonction est bien adaptée pour notre jeu de données.

>> Téléchargez le code source depuis mon espace Github <<

Conclusion

On vient de voir la régression polynomiale en action. Vous vous dites pourquoi j’ai pris un polynôme de degré 4 et non pas de degré 5 ou 6 ou même trois ? je vous invite à essayer différents degrés polynomiaux pour voir ce que ça donne.

N’oubliez pas de partager par un commentaire les résultats que vous avez trouvé 😉

Et si l’article vous plait, n’oubliez pas de le partager. 😉

8 réflexions au sujet de « Régression Polynomiale (Polynomial regression) – Implémentez-la en 10 minutes ! »

Ping : L'apprentissage supervisé - Machine Learning - Apprendre le Machine Learning de A à Z
Ping : 9 Algorithmes de Machine Learning que chaque Data Scientist doit connaitre - Apprendre le Machine Learning de A à Z
Ping : Gradient Descent : Théorie et pratique... La magie du Machine Learning démystifiée ! | Mr. Mint : Apprendre le Machine Learning de A à Z
Simon 8 novembre 2018

Salut Younes, merci pour cet article très clair qui est accessible aux débutants, ce qui est mon cas. J’ai une question sur le degré à choisir pour la fonction polyfit. J’ai essayé différents degrés comme tu l’as conseillé et il est vrai qu’à partir d’un certain degré la régression semble se détacher de la réalité du nuage de points. Je voulais donc savoir comment est ce que l’on explique cela et comment optimiser le choix du degré du polynôme généré par polyfit.
Merci encore

Répondre ↓
1. Younes Benzaki Auteur de l’article28 novembre 2018
  
  Bonjour Simon,
  
  Le changement de degrés du polynome vous donnera un modèle prédictif différent. Généralement, plus on augmente le degré plus le modèle s’adaptera mieux au jeu de données d’apprentissage.
  
  Cette adaptation est bien mais jusqu’à un certain degré car après on tombe dans du overfitting ou underfitting (si le degré du polynome est trop bas). Vous pouvez voir cet article sur le sujet :
  
  https://mrmint.fr/overfitting-et-underfitting-quand-vos-algorithmes-de-machine-learning-derapent
  
  Le choix du « bon » degré du polynôme se fait en découpant le jeu de données en jeu d’entrainement, jeu de validation croisée, et jeu de test. Ainsi, vous pouvez entraîner plusieurs modèles (différents degrés de polynômes) en vous servant du jeu d’entrainement. Les modèles obtenus seront confrontés aux données servant à la validation croisée serviront pour mesurer leur performances. Et on retient le meilleur d’entre eux.
  
  Répondre ↓
HARHOUT 5 janvier 2019

bonjour younes
merci pour cet article qui est très clair. Je cherche un modele multivariable d’ordre n avec interaction des facteurs(paramètres) sous la forme mathematique ex:
p= ∑ ∑ ∑XiYJZk avec i,jetkdes puissances (comment faire varié les indice ijk)

Répondre ↓
martin 3 février 2019

oui sauf qu’ici les points ressemblent plutôt à une fonction du type 1/x , ça se voit très nettement sur le graph final => ça ressemble à rien.

mais merci quand même pour le cour de python !

Répondre ↓
1. Younes Benzaki Auteur de l’article12 février 2019
  
  Bonjour Martin,
  
  Le but de l’article est de montrer « l’adaptabilité » d’une fonction polynomiale à un jeu de données qui n’est pas forcément linéaire. Après, il est possible que le jeu de données est un peu « entassé » ce qui ne reflète pas peut être le but pédagogique de l’article.
  
  Quant à la fonction 1/X (hyperbol), elle se compose de deux « bouts » et est discontinue à 0. On ne peut pas dire que la courbe obtenue ressemble à une fonction 1/X.
  
  Dans un sens plus large, dans une analyse prédictive, on s’intéresse moins à la forme de la fonction du moment qu’elle modélise bien notre jeu de données.
  
  Merci pour votre commentaire constructif.
  
  Répondre ↓

Laisser un commentaire Annuler la réponse

Ce site utilise Akismet pour réduire les indésirables. En savoir plus sur comment les données de vos commentaires sont utilisées.