Dans cet article, je vais implémenter la régression linéaire univariée (à une variable) en python. Le but est de comprendre cet algorithme sans se noyer dans les maths régissant ce dernier.
Il s’agit d’un algorithme d’apprentissage supervisé de type régression. Les algorithmes de régression permettent de prédire des valeurs continues à partir des variables prédictives. Prédire le prix d’une maison en fonction de ses caractéristiques est un bon exemple d’analyse en régression.
La régression linéaire ? De quoi parle t-on ?
Certaines personnes aiment donner des noms compliqués pour des choses intuitives à comprendre. La régression linéaire en est un bon exemple. derrière ce nom, se cache un concept très simple : La régression linéaire est un algorithme qui va trouver une droite qui se rapproche le plus possible d’un ensemble de points. Les points représentent les données d’entraînement (Training Set).
Schématiquement, on veut un résultat comme celui là :
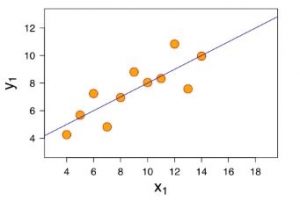
Nos points en orange sont les données d’entrée (input data). Ils sont représentés par le couple ![]() . Les valeurs
. Les valeurs ![]() sont les variables prédictives, et
sont les variables prédictives, et ![]() est la valeur observée (le prix d’une maison par exemple). On cherche à trouver une droite
est la valeur observée (le prix d’une maison par exemple). On cherche à trouver une droite ![]() tel que, quelque soit
tel que, quelque soit ![]() , on veut que
, on veut que ![]() .
.
En d’autres termes, on veut une droite qui soit le plus proche possible de tous les points de nos données d’apprentissage.
Simple, non ?
Implémentons en Python cet algorithme !
Présentation du problème
Le problème qu’on cherche à résoudre ainsi que son jeu de données sont ceux d’un cours que j’ai suivi sur le Machine Learning d’Andrew NG sur Coursera. A l’époque j’ai du implémenter la solution en MATLAB. Je peux vous assurer que ce n’était pas ma tasse de thé. 😉
Le problème à résoudre est le suivant :
Supposons que vous soyez le chef de direction d’une franchise de camions ambulants (Food Trucks). Vous envisagez différentes villes pour ouvrir un nouveau point de vente. La chaîne a déjà des camions dans différentes villes et vous avez des données pour les bénéfices et les populations des villes.
Vous souhaitez utiliser ces données pour vous aider à choisir la ville pour y ouvrir un nouveau point de vente.
Ce problème est de type apprentissage supervisé modélisable par un algorithme de régression linéaire. Il est de type supervisé car pour chaque ville ayant un certain nombre de population (variable prédictive X), on a le gain effectué dans cette dernière (la variable qu’on cherche à prédire : Y).
Format des données
Les données d’apprentissage sont au format CSV. Les données sont séparés par des virgules. La première colonne représente la population d’une ville et la deuxième colonne indique le profit d’un camion ambulant dans cette ville. Une valeur négative indique une perte.
![]()
Le nombre d’enregistrements de nos données d’entrées est 97.
Note : Le fichier est téléchargeable depuis mon espace Github
Pour résoudre ce problème, on va prédire le profit (la variable Y) en fonction de la taille de la population (la variable prédictive X)
Chargement des données
Tout d’abord, il faudra lire et charger les données contenues dans le fichier CSV. Python propose via sa librairie Pandas des classes et fonctions pour lire divers formats de fichiers dont le CSV.
import pandas as pd
df = pd.read_csv("D:\DEV\PYTHON_PROGRAMMING\univariate_linear_regression_dataset.csv")
La fonction read_csv(), renvoie un DataFrame. Il s’agit d’un tableau de deux dimensions contenant, respectivement, la taille de population et les profits effectués. Pour pouvoir utiliser les librairies de régression de Python, il faudra séparer les deux colonnes dans deux variables Python.
#selection de la première colonne de notre dataset (la taille de la population) X = df.iloc[0:len(df),0] #selection de deuxième colonnes de notre dataset (le profit effectué) Y = df.iloc[0:len(df),1]
Les variables X et Y sont maintenant de simples tableaux contenant 97 éléments.
Note :
- La fonction len() permet d’obtenir la taille d’un tableau
- La fonction iloc permet de récupérer une donnée par sa position
- iloc[0:len(df),0] permettra de récupérer toutes les données de la ligne 0 à la ligne 97 (qui est len(df)) se trouvant à la colonne d’indice 0
Visualisation des données
Avant de modéliser un problème de Machine Learning, il est souvent utile de comprendre les données. Pour y arriver, on peut les visualiser dans des graphes pour comprendre leur dispersion, déduire les corrélations entre les variables prédictives etc…
Parfois, il est impossible de visualiser les données car le nombre de variables prédictives est trop important. Ce n’est pas le cas ici, on ne dispose que de deux variables : la population et les profits.
Nous pouvons utiliser un graphe de type nuage de points (Scatter plot) pour visualiser les données :
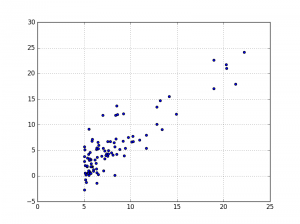
On voit clairement qu’il y a une corrélation linéaire entre les variables. Et que plus la taille de la population augmente, plus le profit en fait de même.
Le code Python permettant d’effectuer ce nuage de points est le suivant :
import matplotlib.pyplot as plt axes = plt.axes() axes.grid() # dessiner une grille pour une meilleur lisibilité du graphe plt.scatter(X,Y) # X et Y sont les variables qu'on a extraite dans le paragraphe précédent plt.show()
Note :
- Matplotlib est la librairie python permettant de faire des graphes de plusieurs types :
- Histogrammes
- Nuages de Points,
- Dessiner des courbes de fonctions
- Des schémas camembert (Pie plot)
- etc…
Appliquer l’algorithme
Maintenant qu’on comprend mieux nos données, nous allons attaquer le cœur du problème : Trouver une fonction prédictive ![]() qui prendra en entrée une taille de population, et produira en sortie une estimation du gain espéré. L’idée du jeu est que la prédiction soit proche de la valeur observée
qui prendra en entrée une taille de population, et produira en sortie une estimation du gain espéré. L’idée du jeu est que la prédiction soit proche de la valeur observée ![]() .
.
Note : Par souci de simplicité, j’ai fait le choix de ne pas découper mes données issues du fichier CSV en Training Set et Test Set. Cette bonne pratique, à appliquer dans vos problématiques ML, permet d’éviter le sur-apprentissage. Dans cet article, nos données serviront à la fois à l’entrainement de notre algorithme de régression et aussi comme jeu de test.
Pour utiliser la régression linéaire à une variable (univariée), on utilisera le module scipy.stats. Ce dernier dispose de la fonction linregress, qui permet de faire la régression linéaire.
from scipy import stats #linregress() renvoie plusieurs variables de retour. On s'interessera # particulierement au slope et intercept slope, intercept, r_value, p_value, std_err = stats.linregress(X, Y)
Effectuer des prédictions
Après que la fonction linregress() nous ait renvoyé les paramètres de notre modèle : ![]() et
et ![]() , on pourra effectuer des prédictions. En effet, la fonction de prédiction sera de la forme :
, on pourra effectuer des prédictions. En effet, la fonction de prédiction sera de la forme :
On peut écrire cette fonction ![]() en python comme suit :
en python comme suit :
def predict(x): return slope * x + intercept
Grâce à cette fonction, on peut effectuer une prédiction sur nos 97 populations ce qui nous fera une ligne droite.
#la variable fitLine sera un tableau de valeurs prédites depuis la tableau de variables X fitLine = predict(X) plt.plot(X, fitLine, c='r')
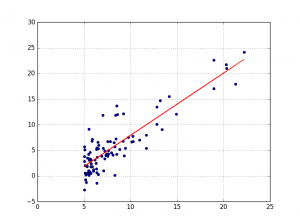
En effet, on voit bien que la ligne rouge, approche le plus possible tous les points du jeu de données. Joli non ? 🙂
Si on prend par hasard, la 22 ème ligne de notre fichier CSV, on a la taille de population qui fait : 20.27 * 10 000 personnes et le gain effectué était : 21.767 * 10 000 $
En appelant la fonction predict() qu’on a défini précédemment :
print predict(20.27) # retourne : 20.3870988313
On obtient un gain estimé proche du vrai gain observé (avec un certain degré d’erreur)
>> Téléchargez le code source depuis Github <<
Résumé
Dans cet article, nous avons implémenté en Python la régression linéaire univariée. Nous avons vu comment visualiser nos données par des graphes, et prédire des résultats.
Pour garder l’exemple simple, je n’ai pas abordé les notions de découpage du jeu données en Training Set et Test Set. Cette bonne pratique permet d’éviter le phénomène de sur-apprentissage.
Toujours pour garder l’exemple simple, je n’ai pas parlé d’évaluation du modèle. Cette notion permet de savoir si le modèle produit est représentatif et généralisable à des données non encore vu par notre algorithme.
Tous ces éléments feront l’objet d’articles futurs.
Si vous avez des questions, n’hésitez pas à me les poser dans un commentaire et si l’article vous plait, n’oubliez pas de le faire partager ! 😉

Ping : Implémenter la régression linéaire multivariée en Python - Apprendre le Machine Learning de A à Z
Ping : Gradient Descent : Théorie et pratique... La magie du Machine Learning démystifiée ! - Apprendre le Machine Learning de A à Z
Ping : 10 minutes pour comprendre la régression polynomiale - Apprendre le Machine Learning de A à Z
Ping : 9 Algorithmes de Machine Learning que chaque Data Scientist doit connaitre - Apprendre le Machine Learning de A à Z
pourquoi t’as pas utilisé sckit-learn? Puis c’est quoi la difference entre scikit-learn et scipy?
Bonjour enock,
La régression linéaire est un avant tout un procédé statistique qui a été emprunter de cette discipline pour en faire un algorithme de Machine Learning. Il n’est donc pas choquant de une implémentation de la régression linéaire dans scipy qui se veut un module de calcule scientifique.
Scikit Learn quant à elle est une librairie de Machine Learning. Et comme il existe un « algorithme » de régression linéaire dans la sphère ML, il ont définit également une classe permettant ce calcul.
Laquelle utiliser ?
je dirai que les résultats seront sensiblement les mêmes. A toi d’utiliser celle qui te convient le plus.
Bonjour, pourrais-je entrer en contact avec vous svp?
Bonjour,
j’ai vraiment apprecié le travail, mais pouvez vous utiliser un fichier excel au lieu d’un fichier CSV ?
Bonjour moussdiall,
Je te remercie pour ton commentaire 🙂
la raison de ma préférence pour les CSV est la simplicité de leur format. Comme vous l’avez vu, une seule instruction Pandas permet de charger le fichier CSV.
Egalement, je préfère ce format pour ne pas encombrer les lecteurs par des détails techniques de lecture d’un fichier excel.
Toutefois, il existe plusieurs librairies pour lire un fichier excel. Je vous conseille la librairie « xlrd ». vous trouverez un exemple de chargement de données excel depuis python à cette url : https://www.blog.pythonlibrary.org/2014/04/30/reading-excel-spreadsheets-with-python-and-xlrd/
Finalement, que ce soit des csv ou excel ou des bases de données relationnelles, le procédé d’apprentissage d’un algorithme ML reste la même.
Bonjour,
J’arrive pas à télécharger le fichier depuis l’espace Github?
Bonjour
Il faut créer un compte github et cliquer sur le bouton « download » du projet concerné ou faire un « git clone » si vous disposez de Git
Bonne journée
Bonjour, Merci pour ces informations précieux.
Pouvez-vous partagez avec moi le lien du fichier CSV? Je l’ai pas trouvé.
Bonjour Asmae,
Vous pouvez récupérer l’ensemble du projet qui est sur Github en faisant un « git clone » du projet.
Si vous n’y arrivez pas, voici le lien du fichier CSV :
https://github.com/ybenzaki/univariate_linear_regression_python/blob/master/univariate_linear_regression_dataset.csv
Il suffit de le télécharger comme n’importe quel autre fichier.
Bonne journée 🙂
Bonjour,
J’ai eut une erreur de calcul entre float et integer dans la fonction
j’ai alors modifié le prog comme suit :
fitLine = [i*slope +intercept for i in X]
pour la def de filLine
et j’ai viré la fonction au début
plus simple du coup
Bonjour,
Cette régression ne marche pas avec des valeurs non entières ?
merci
Bonjour Aurélien,
une régression linéaire fonctionne aussi bien sur des valeurs entières que non entières. Elle est mal adaptée si les valeurs sont des modalités (des valeurs discrètes) comme le sexe d’une personne, couleur de yeux …etc (même si ces modalités sont encodées dans des valeurs numériques).
Bien à vous
Ping : Data scientist : faites grimper votre salaire en 2020 • HIDDEN MARKET