Dans cet article, on verra comment fonctionne L’algorithme de Gradient (Gradient Descent Algorithm) pour calculer les modèles prédictifs.
Depuis quelques temps maintenant, je couvrais la régression linéaire, univariée, multivariée, et polynomiale. Tout au long de ces articles, je parlais de fonction/modèle prédictif. Mais je ne m’étais jamais attardé à expliquer comment se calcule la fonction de prédiction fournie par les librairies ML.
Dans cet article, on va démystifier la magie qui se produit pour calculer nos modèles prédictifs !
Note 1 : Pour mieux suivre cet article, je vous conseille de lire ce que c’est la régression linéaire univariée.
Note 2 : Les notions abordées dans cet article sont intrinsèquement liées aux mathématiques. Accrochez-vous ! il se peut que vous soyez secoué un peu !
Note 3 : Les notions abordées dans cet article sont généralement déjà implémentées dans les librairies de Machine Learning. Vous n’aurez pas à les coder par vous même. Mais il est toujours utile de les comprendre pour avoir des bases solides en ML.
Régression linéaire univariée : Le Rappel !
La régression linéaire univariée est un algorithme prédictif supervisé. Il prend en entrée une variable prédictive ![]() et va essayer de trouver une fonction de prédiction
et va essayer de trouver une fonction de prédiction ![]() . Cette fonction sera une droite qui s’approchera le plus possible des données d’apprentissage. La fonction de prédiction étant une droite, elle s’écrira mathématiquement sous la forme :
. Cette fonction sera une droite qui s’approchera le plus possible des données d’apprentissage. La fonction de prédiction étant une droite, elle s’écrira mathématiquement sous la forme :
Avec :
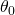 et
et 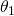 sont les coefficients de la droite.
sont les coefficients de la droite.
regression lineaire
La droite en rouge représente la meilleure approximation par rapport au nuage de points bleus. Cette approximation est rendue possible par ce qu’on a pu calculer les paramètres prédictifs ![]() et
et ![]() qui définissent notre droite rouge.
qui définissent notre droite rouge.
La question qui se pose est : Comment on calcule les valeurs de ![]() et
et ![]() ?
?
La fonction de coût d’erreur (Cost Function)
La figure en haut montre que la droite en rouge tente d’approcher le plus de points possibles (en réduisant l’écart avec ces derniers). En d’autres termes, elle minimise au maximum l’erreur globale.
Pour la régression linéaire univariée, nous avons vu que la fonction de prédiction s’écrivait ainsi :
Le but du jeu revient à trouver un couple (![]() ,
,![]() ) optimal tel que
) optimal tel que ![]() soit le plus proche possible de
soit le plus proche possible de ![]() (la valeur qu’on essaie de prédire). Et ce, pour tous les couples
(la valeur qu’on essaie de prédire). Et ce, pour tous les couples ![]() qui forment notre ensemble de données d’apprentissage.
qui forment notre ensemble de données d’apprentissage.
Note : pensez à ![]() comme un imitateur de
comme un imitateur de ![]() . La fonction
. La fonction ![]() va essayer de transformer au mieu
va essayer de transformer au mieu ![]() en
en ![]() tel que
tel que ![]() .
.
Note : on définit « l‘erreur unitaire » entre une valeur observée ![]() et une valeur prédite
et une valeur prédite ![]() , comme suit :
, comme suit :
![]()
Trouver le meilleur couple (![]() ,
,![]() ) revient à minimiser le coût global des erreurs unitaires qui se définit comme suit :
) revient à minimiser le coût global des erreurs unitaires qui se définit comme suit :
![]()
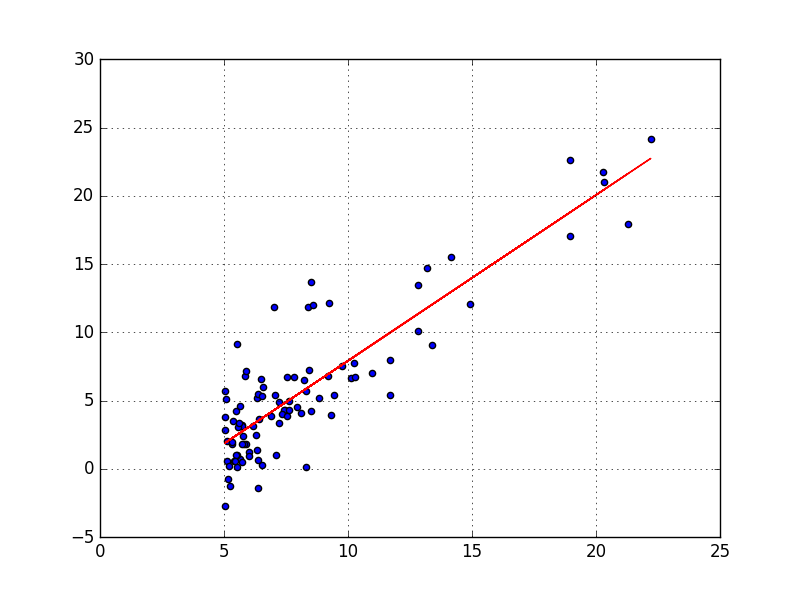
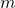 est la taille du training set
est la taille du training set
La fonction de coût est définie comme suit :
![]()
En remplaçant le terme ![]() par sa valeur on obtient :
par sa valeur on obtient :
![]()
Cette formule représente la fonction de coût (cost function / Error function) pour la régression linéaire univariée.
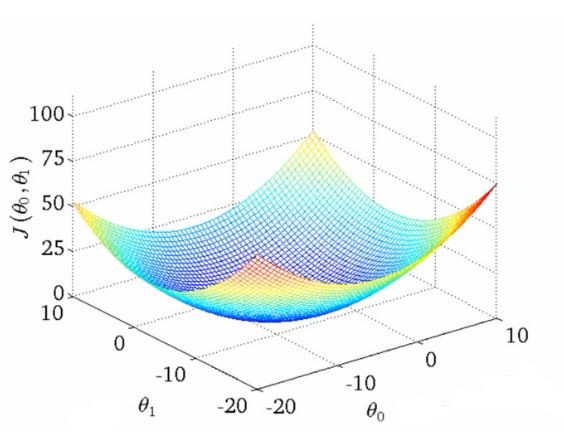
Gradient Descent visualisation
Trouver les meilleurs paramètres
et
revient à minimiser (trouver le minimum) la fonction du coût.
Visuellement, on remarque que la fonction ![]() a la forme d’un bol. Mathématiquement, on dit que la fonction convexe. La convexité d’une fonction implique que cette dernière possède un seul minimum global. Les valeurs de
a la forme d’un bol. Mathématiquement, on dit que la fonction convexe. La convexité d’une fonction implique que cette dernière possède un seul minimum global. Les valeurs de ![]() et
et ![]() qui sont au minimum global de
qui sont au minimum global de ![]() seront les meilleures valeurs pour notre hypothèse
seront les meilleures valeurs pour notre hypothèse ![]() .
.
Minimisation de la fonction de coût 
Une façon de calculer le minimum de la fonction de coût ![]() est d’utiliser l’algorithme : la descente du gradient (Gradient descent). Ce dernier est un algorithme itératif qui va changer, à chaque itération, les valeurs de
est d’utiliser l’algorithme : la descente du gradient (Gradient descent). Ce dernier est un algorithme itératif qui va changer, à chaque itération, les valeurs de ![]() et
et ![]() jusqu’à trouver le meilleur couple possible.
jusqu’à trouver le meilleur couple possible.
l’algorithme se décrit comme suit :
Début de l’algorithme : Gradient Descent
Initialiser aléatoirement les valeurs de :et
répéter jusqu’à convergence au minimum global de la fonction de coût
pour
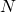
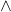
retourner
et
Fin algorithme
L’algorithme peut sembler compliqué à comprendre, mais l’intuition derrière est assez simple:
Imaginez que vous soyez dans une colline, et que vous souhaitez la descendre. A chaque nouveau pas (analogie à l’itération), vous regardez autour de vous pour trouver la meilleure pente pour avancer vers le bas. Une fois la pente trouvée, vous avancez d’un pas d’une grandeur ![]() .
.
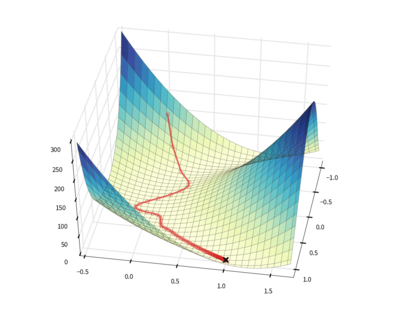
Gradient Descent algorithm
Dans la définition de l’algorithme on remarque ces deux termes :
- le terme
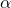 s’appelle le Learning Rate : il fixe la « grandeur » du pas de chaque itération du Gradient Descent.
s’appelle le Learning Rate : il fixe la « grandeur » du pas de chaque itération du Gradient Descent. 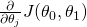 : Ce terme est la dérivée partielle pour chacun des termes
: Ce terme est la dérivée partielle pour chacun des termes 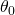 et
et 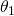 .
.
Pour les matheux, vous pouvez calculer les dérivées partielles de ![]() ,
,![]() . Sinon, les voici :
. Sinon, les voici :
A chaque itération, l’algorithme avancera d’un pas et trouvera un nouveau couple de ![]() et
et ![]() . Et à chaque itération, le coût d’erreur global se réduira.
. Et à chaque itération, le coût d’erreur global se réduira.
Implémenter le Gradient Descent
Assez de gavage théorique, et codons cet algorithme pour mieux en comprendre les subtilités. On sait comment calculer les dérivées partielles, et on dispose du jeu de données de l’article sur la régression univariée.
Charger les données d’apprentissage
df = pd.read_csv("D:\DEV\PYTHON_PROGRAMMING\coursera_ml_exercices_in_python\univariate_linear_regression_dataset.csv")
X = df.iloc[0:len(df),0]#une seule variable prédictive car régression univarié
Y = df.iloc[0:len(df),1]#Valeurs observées (à prédire)
# la taille de notre ensemble de données d'apprentissage
Calculer les dérivées partielles
Rappelons nous que la fonction de coût est définie comme suit :
![]()
Les dérivées partielles de ![]() et
et ![]() sont :
sont :
L’implémentation en Python de ces dérivées partielles est le suivant :
M = len(X)
def calculer_derivees_partielles(ancien_theta_0, ancien_theta_1):
derivee_theta_0 = float(0)
derivee_theta_1 = float(0)
for i in range(0, len(X)):
derivee_theta_0 += float(((ancien_theta_0 + (ancien_theta_1 * X[i])) - float(Y[i])))
derivee_theta_1 += (((ancien_theta_0 + (ancien_theta_1 * X[i]))) - float(Y[i])) * float(X[i])
derivee_theta_0 = (1/M) * derivee_theta_0
derivee_theta_1 = (1/M) * derivee_theta_1
return [derivee_theta_0, derivee_theta_1]
Mise à jour des valeurs de 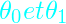
Maintenant qu’on a notre fonction qui calcule les dérivées partielles, on peut à présent mettre en place l’instruction qui fera la mise à jour des valeurs de ![]() et
et ![]()
def calculer_nouvelles_theta(ancien_theta_0, ancien_theta_1):
[derivee_theta_0, derivee_theta_1] = calculer_derivees_partielles(ancien_theta_0,ancien_theta_1)
nouvelle_theta_0 = ancien_theta_0 - (learning_rate_ALPHA * derivee_theta_0)
nouvelle_theta_1 = ancien_theta_1 - (learning_rate_ALPHA * derivee_theta_1)
return [nouvelle_theta_0,nouvelle_theta_1]
les paramètres qu’on passe à la fonction calculer_nouvelles_theta sont les ![]() et
et ![]() qu’on a calculé lors de la tour de boucle précédente.
qu’on a calculé lors de la tour de boucle précédente.
Mise en place et lancement de Gradient Descent
Tous les ingrédients sont là pour implémenter Gradient descent, en voila une implémentation :
learning_rate_ALPHA = float(0.0001)
initial_theta_0 = float(0)
initial_theta_1 = float(0)
nombre_iterations = 2000
def lancer_gradient_descent():
tmp_theta_0 = initial_theta_0
tmp_theta_1 = initial_theta_1
for i in range(nombre_iterations):
[nouvelle_theta_0, nouvelle_theta_1] = calculer_nouvelles_theta(tmp_theta_0, tmp_theta_1)
tmp_theta_0 = nouvelle_theta_0
tmp_theta_1 = nouvelle_theta_1
return [tmp_theta_0, tmp_theta_1]
[final_theta_0, final_theta_1] = lancer_gradient_descent()
print "After {0} iterations theta_0 = {1}, theta_1 = {2}".format(nombre_iterations, final_theta_0, final_theta_1)
Quelques remarques sur Gradient Descent
On vient d’implémenter l’algorithme Gradient Descent. Ce dernier tente de réduire, à chaque itération le coût global d’erreur et ce en minimisant la fonction ![]() ,
,![]() . On peut s’en assurer en regardant comment évolue les valeurs de
. On peut s’en assurer en regardant comment évolue les valeurs de ![]() ,
,![]() au cours des itérations.
au cours des itérations.
def calculer_cost_function(theta_0, theta_1):
global_cost = 0
for i in range(len(X)):
cost_i = ((theta_0 + (theta_1 * X[i])) - Y[i]) * ((theta_0 + (theta_1 * X[i])) - Y[i])
global_cost+= cost_i
return (1/ (2 * len(X))) * global_cost
xx = []; yy=[]
axes = plt.axes()
axes.grid()
#dessiner l'avancer des differents de J(theta_0, theta_1)
for i in range(len(COST_RECORDER)):
xx.append(i)
yy.append(COST_RECORDER[i])
plt.scatter(xx,yy)
plt.show()
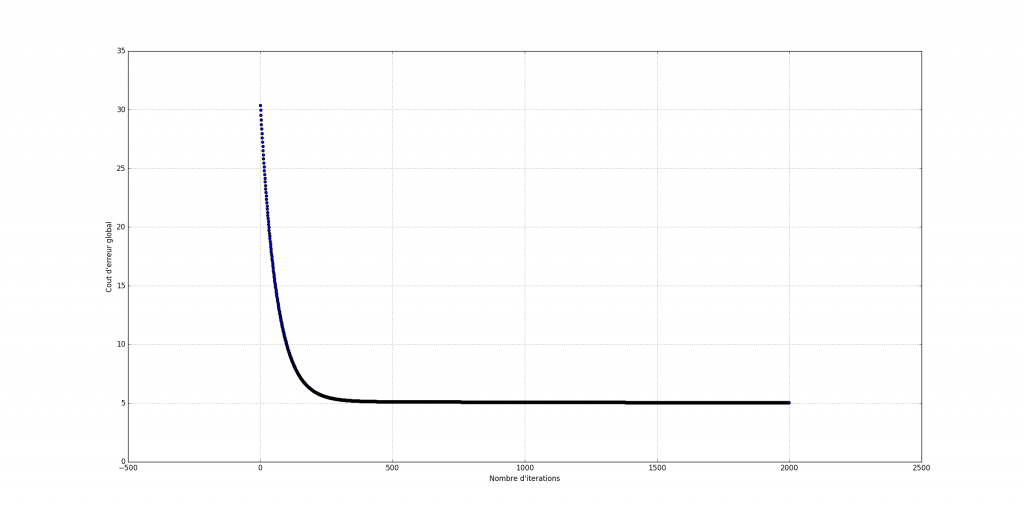
cost function minimization
On remarque qu’au bout d’un certain nombre d’itérations, Gradient se stabilise ainsi que le coût d’erreur global ![]() . Sa stabilisation indique une convergence de l’algorithme.
. Sa stabilisation indique une convergence de l’algorithme.
>> Téléchargez le code source depuis Github <<
Conclusion
On vient de voir comment l’algorithme Gradient Descent opère. Ce dernier est un must know en Machine Learning. Par souci de simplicité, j’ai implémenté Gradient Descent avec la régression linéaire univariée. Mais la même logique s’applique pour d’autres modèles Machine Learning. Notamment : la régression logistique, régression polynomiale, SVM etc…
Toutefois, Rassurez vous, vous n’aurez pas à implémenter la descente du Gradient par vous même. Les librairies de Machine Learning font tout ça pour vous. Mais il est toujours utile de comprendre ce qui se passe derrière pour mieux interpréter les modèles fournis par ces libraires.
Si vous avez des questions, n’hésitez pas à me les poser dans un commentaire et si l’article vous plait, n’oubliez pas à le faire partager ! 😉

Ping : 9 Algorithmes de Machine Learning que chaque Data Scientist doit connaitre - Apprendre le Machine Learning de A à Z
Ping : Overfitting et Underfitting : Quand vos algorithmes de Machine Learning dérapent ! - Apprendre le Machine Learning de A à Z
Veuillez publier des exemples de calcul
Bonjour Sara,
Tu pourras retrouver l’implémentation du code de Gradient Descent en Python (version 2) sur mon repository Github (le lien en rouge en bas de l’article).
Je te suggère de le téléchager, et le lancer. Pour voir l’évolution des valeurs de theta0 et theta1 tu peux faire des appels à la fonction print de python pour voir ce que fait l’algorithme lors de son fonctionnement.
Hello,
Merci beaucoup pour tes articles , j’ai passé le mooc coursera avec Andrew et cet article est un tres bon support pour moi
Hello,
Merci pour ton retour 🙂
Bonjour Monsieur,
Moi mon sujet de mémoire était deep learning pour la résolution des problèmes stochastiques .Au bout de deux semaines mon encadreur se rend compte qu’il ma pas donné les bons documents. A présent , il veut que je travaille sur l’analyse de l erreur de la méthode de gradient de descente. Je vais essayer de regarder vos pages sur le deep learning un peu.
J’ ai aussi un soucis pourquoi votre fonction de coût il y’a une division sur 2*m
Bonjour Mbanta,
La fonction de coût définie dans l’article est reprise de plusieurs littérature sur le Machine Learning. La division par 1/m permet d’avoir la moyenne des erreurs au carré. par ailleurs le 1/2 est faite pour des considérations de calculs de dérivées partielles pour mettre à jour les valeurs des théta.
Dans les fait, 1/2 étant une constante, cela n’a pas d’incidence sur le résultat de minimisation de la fonction J.
C’est vraiment trés interessant Merci encore!!
Avec plaisir ! Merci pour le commentaire 🙂