Les données sont au centre des algorithmes de Machine Learning. Par conséquent, préparer au mieux ces données, permettra d’avoir de meilleures performances.
La plupart du temps, en machine Learning, les Data Set proviennent avec des ordres de grandeurs différents. Cette différence d’échelle peut conduire à des performances moindres. Pour palier à cela, des traitements préparatoires sur les données existent. Notamment le Feature Scaling qui comprend la Standardisation et la Normalisation.
Voyons de plus prêt ces notions.
C’est parti !

Data preprocessing
Nécessité de faire du Data preprocessing
Quand les données d’un Data Set sont dans des ordres de grandeurs différents, certains algorithmes de Machine Learning mettent plus de temps à trouver un modèle prédictif optimal.
Trouver un modèle prédictif optimal, revient souvent à minimiser une fonction de coût (en utilisant Gradient Descent par exemple). Ce dernier va itérativement, trouver un vecteur de poids (weights) ![]() , qui minimise la fonction de coût.
, qui minimise la fonction de coût.
Supposons qu’on ait à prédire le prix d’une maison en fonction de sa superficie et le nombre de chambres qu’elle contient. La feature nombre de chambres sera largement inférieure à la superficie de l’appartement (ex : 40 M² pour 2 pièces).
Pour une régression multivariée, vu qu’on a pour cet exemple deux features (![]() : la superficie et
: la superficie et ![]() : le nombre de chambres), on aura à trouver trois constantes
: le nombre de chambres), on aura à trouver trois constantes ![]() ,
, ![]() , et
, et ![]() .
.
Tel que :
![]()
Note : ![]() vaut toujours 1. Il s’agit d’une astuce mathématique pour simplifier le calcul matriciel de
vaut toujours 1. Il s’agit d’une astuce mathématique pour simplifier le calcul matriciel de ![]() . Pour plus d’informations, voir l’article sur comment sont représentées les features en Machine Learning
. Pour plus d’informations, voir l’article sur comment sont représentées les features en Machine Learning
Lors des itérations du gradient Descent pour calculer les meilleurs ![]() pour
pour ![]() , certaines d’entre elles se mettront plus rapidement à jour par rapport à d’autres. Cela en fonction de l’ordre de grandeur des différentes features. Cette différence de « rapidité » de mise à jour des
, certaines d’entre elles se mettront plus rapidement à jour par rapport à d’autres. Cela en fonction de l’ordre de grandeur des différentes features. Cette différence de « rapidité » de mise à jour des ![]() , conduira à ce que Gradient Descent mette plus de temps pour converger et par conséquent trouver le modèle optimal.
, conduira à ce que Gradient Descent mette plus de temps pour converger et par conséquent trouver le modèle optimal.
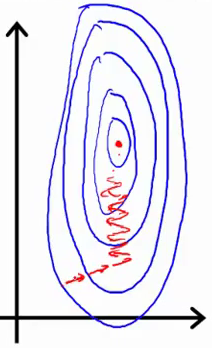
Illustration inspirée du cours d’Andrew NG
Le contour plot ci-dessus est typique de deux features ayant une grandeur d’échelle différentes. On remarque que les contours (lignes bleues) sont assez entassées. Les flèches rouges illustrent comment Gradient Descent peine (avec des « zig-zag ») à trouver le « centre » du contour plot qui est le vecteur ![]() optimal.
optimal.
On remarque également, avec les flêches rouges, que le Gradient Descent, met plus d’itérations pour trouver le centre du « contour plot » qui est le meilleur couple de ![]() et
et ![]() .
.
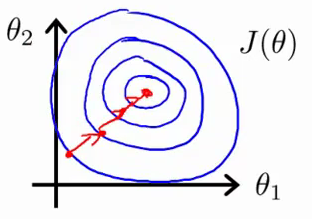
Illustration inspirée du cours d’Andrew NG
En appliquant la normalisation, on souhaite obtenir une valeur de features ayant le même ordre de grandeur (on y vient dans la suite de l’article). La première conséquence à cela est d’avoir un contour plot plus régulier (et moins entassé). Généralement, dans cette situation, Gradient Descent trouve plus rapidement le minimum de la fonction de coût. Et par conséquent la fonction de prédiction optimale.
Les algorithmes concernés par le Data processing
Le Feature Scaling est une bonne pratique, pour ne pas dire obligatoire, lors de la modélisation avec du Machine Learning.
Les algorithmes pour lesquels le feature scaling s’avère nécessaire, sont ceux pour lesquels il faudra
- Calculer un vecteur de poids (weights) theta
- Calculer des distances pour déduire le degrée de similarité de deux items
- Certains algorithmes de Clustering
Plus concrétement, voici une liste d’algorithmes non exhaustive pour lesquels il faudra procéder au Feature Scaling :
- Logistic Regression
- Regression Analysis (polynomial, multivariate regression…)
- Support Vector Machines (SVM)
- K-Nearest Neighbors (KNN)
- K-Means (clustering…)
- Principal Component Analysis (PCA)
Les différentes techniques de Feature Scaling
La Normalisation
Min-Max Scaling peut- être appliqué quand les données varient dans des échelles différentes. A l’issue de cette transformation, les features seront comprises dans un intervalle fixe [0,1]. Le but d’avoir un tel intervalle restreint est de réduire l’espace de variation des valeurs d’une feature et par conséquent réduire l’effet des outliers.
La normalisation peut- être effectuée par la technique du Min-Max Scaling. La transformation se fait grâce à la formule suivante :
![]()
Avec :
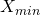 : la plus petite valeur observée pour la feature X
: la plus petite valeur observée pour la feature X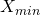 : la plus grande valeur observée pour la feature X
: la plus grande valeur observée pour la feature X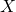 : La valeur de la feature qu’on cherche à normaliser
: La valeur de la feature qu’on cherche à normaliser
La Standardisation
La standardisation (aussi appelée Z-Score normalisation à ne pas confondre avec la normalisation du paragraphe précendent) peut- être appliquée quand les input features répondent à des distributions normales (Distributions Gaussiennes) avec des moyennes et des écart-types différents. Par conséquent, cette transformation aura pour impact d’avoir toutes nos features répondant à la même loi normale ![]() .
.
La standardisation peut également être appliquée quand les features ont des unités différentes.
La Standardisation est le processus de transformer une feature en une autre qui répondra à la loi normale (Gaussian Distribution) ![]() avec :
avec :
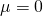 La moyenne de la loi de distribution
La moyenne de la loi de distribution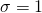 est l’Écart-type (Standard Deviation)
est l’Écart-type (Standard Deviation)
La formule de standardisation d’une feature est la suivante :
avec :
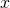 la valeur qu’on veut standardiser (input variable)
la valeur qu’on veut standardiser (input variable)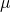 la moyenne (mean) des observations pour cette feature
la moyenne (mean) des observations pour cette feature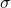 est l’ecart-type (Standard Deviation) des observations pour cette feature
est l’ecart-type (Standard Deviation) des observations pour cette feature
Pour s’assurer que nos données non transformées répondent à une loi normale, on peut toujours faire un plot pour voir leur répartition.
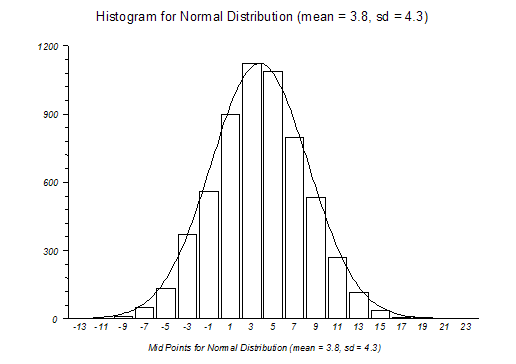
Exemple de données répondant à une loi normal ![]()
Feature Scaling et Scikit Learn
Python et sa librairie Sickit Learn permettent d’appliquer le feature scaling sans avoir à coder les formules par nous même. Les fonctions de feature scaling sont regroupées dans le package preprocessing de Sickit Learn.
Dans cette section, on appliquera la normalisation et la standardisation sur un jeu de données et verront les impacts de ces transformations à l’aide de visualisations graphique.
A propos du jeu de données
Le jeu de données computer Hardware qu’on va utiliser est publié par l’université américaine UCI. C’est un jeu de données qui a été utilisé pour des besoins de recherche notamment en Regression Analysis.
Vous pouvez trouver une description complète de la composition du dataset à cette adresse.
Pour simplifier la lecture des snippets de code, je suivrai la démarche suivante :
- Chargement du dataset
- Application d’une technique de feature scaling
- Affichage de certaines métriques (notamment le min, le max et la moyenne)
Pour les besoins illustratifs, je m’interesserai uniquement aux features MYCT et MMAX. Elles représentent respectivement :
- MYCT : Machine Cycle time in nanoseconds
- MMAX : Maximum Main Memory in Kilobytes
On remarque déjà qu’on a une différence d’unités 🙂
Application de la normalisation
La normalisation peut- être appliquée par le min-max scaling. Python propose pour cela une classe nommée « MinMaxScaler » dans le package preprocessing.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/cpu-performance/machine.data'
names= ['constructor','Model','MYCT','MMIN','MMAX','CACH','CHMIN','CHMAX','PRP','ERP']
dataset = pd.read_csv(url, names=names)
# MIN MAX SCALING
minmax_scale = MinMaxScaler().fit(dataset[['MYCT', 'MMAX']])
df_minmax = minmax_scale.transform(dataset[['MYCT', 'MMAX']])
#imprimer un retour à la ligne pour une meilleur clarete de lecture
print('\n********** Normalisation*********\n')
print('Moyenne apres le Min max Scaling :\nMYCT={:.2f}, MMAX={:.2f}'
.format(df_minmax[:,0].mean(), df_minmax[:,1].mean()))
print('\n')
print('Valeur minimale et maximale pour la feature MYCT apres min max scaling: \nMIN={:.2f}, MAX={:.2f}'
.format(df_minmax[:,0].min(), df_minmax[:,0].max()))
print('\n')
print('Valeur minimale et maximale pour la feature MMAX apres min max scaling : \nMIN={:.2f}, MAX={:.2f}'
.format(df_minmax[:,1].min(), df_minmax[:,1].max()))
L’exécution de ce code produit l’affichage suivant :
********** Normalisation********* Moyenne apres le Min max Scaling : MYCT=0.13, MMAX=0.18 Valeur minimale et maximale pour la feature MYCT apres min max scaling: MIN=0.00, MAX=1.00 Valeur minimale et maximale pour la feature MMAX apres min max scaling : MIN=0.00, MAX=1.00 Affichage des valeurs apres scaling [[ 0.07282535 0.09284284] [ 0.00809171 0.4994995 ] [ 0.00809171 0.4994995 ] ..., [ 0.07282535 0.12412412] [ 0.31220499 0.12412412] [ 0.31220499 0.06156156]]
On remarque bien qu’après la normalisation, l’intervalle des valeurs devient limité entre 0 et 1. Cela est vrai pour les deux features.
Application de la standardisation
Pour appliquer la standardisation, on peut utiliser la classe StandardScaler de Sickit Learn.
********** Normalisation*********</pre>
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/cpu-performance/machine.data'
names= ['constructor','Model','MYCT','MMIN','MMAX','CACH','CHMIN','CHMAX','PRP','ERP']
dataset = pd.read_csv(url, names=names)
# Z-Score standardisation
std_scaler = MinMaxScaler().fit(dataset[['MYCT', 'MMAX']])
df_std = std_scaler.transform(dataset[['MYCT', 'MMAX']])
print('\n********** Standardisation*********\n')
print('Moyenne et Ecart type apres la standardisation de la feature MYCT :\nMoyenne={:.2f}, Ecart Type={:.2f}'
.format(df_std[:,0].mean(), df_std[:,0].std()))
print('\n')
print('Moyenne et Ecart type apres la standardisation de la feature MYCT :\nMoyenne={:.2f}, Ecart Type={:.2f}'
.format(df_std[:,1].mean(), df_std[:,1].std()))
print('\n')
print('Valeur minimale et maximale pour la feature MYCT apres min max scaling: \nMIN={:.2f}, MAX={:.2f}'
.format(df_std[:,0].min(), df_std[:,0].max()))
print('\n')
print('Valeur minimal et maximal pour la feature MMAX apres min max scaling : \nMIN={:.2f}, MAX={:.2f}'
.format(df_std[:,1].min(), df_std[:,1].max()))
print('Affichage des valeurs apres scaling')
print(df_std)
L’exécution de ce code produit l’affichage suivant :
********** Standardisation********* Moyenne et Ecart type apres la standardisation de la feature MYCT : Moyenne=0.13, Ecart Type=0.18 Moyenne et Ecart type apres la standardisation de la feature MYCT : Moyenne=0.18, Ecart Type=0.18 Valeur minimale et maximale pour la feature MYCT apres min max scaling: MIN=0.00, MAX=1.00 Valeur minimal et maximal pour la feature MMAX apres min max scaling : MIN=0.00, MAX=1.00 Affichage des valeurs apres scaling [[ 0.07282535 0.09284284] [ 0.00809171 0.4994995 ] [ 0.00809171 0.4994995 ] ..., [ 0.07282535 0.12412412] [ 0.31220499 0.12412412] [ 0.31220499 0.06156156]]
Représentation graphique des données avant et après normalisation
Pour mieux appréhender l’impact des techniques de features scaling sur les données, nous allons dessiner un plot visualisant nos deux features avant et après l’application de la standardisation et la normalisation.
Par souci de simplicité, j’ai regroupé dans une seule fonction l’affichage des trois données (sans transformation, données après normalisation et données après Standardisation).
def plot():
plt.figure(figsize=(8,6))
plt.scatter(dataset['MYCT'], dataset['MMAX'],
color='green', label='donnees sans transformations', alpha=0.5)
plt.scatter(df_minmax[:,0], df_minmax[:,1],
color='red', label='min-max scaled [min=0, max=1]', alpha=0.3)
plt.scatter(df_std[:,0], df_std[:,1],
color='blue', label='Standardisation vers la loi Normal X ~ N(0,1)', alpha=0.3)
plt.title('Plot des features MYCT et MMAX avant et apres scaling')
plt.xlabel('MYCT')
plt.ylabel('MMAX')
plt.legend(loc='upper right')
plt.grid()
plt.tight_layout()
plot()
plt.show()
Ce qui produira la figure suivante :
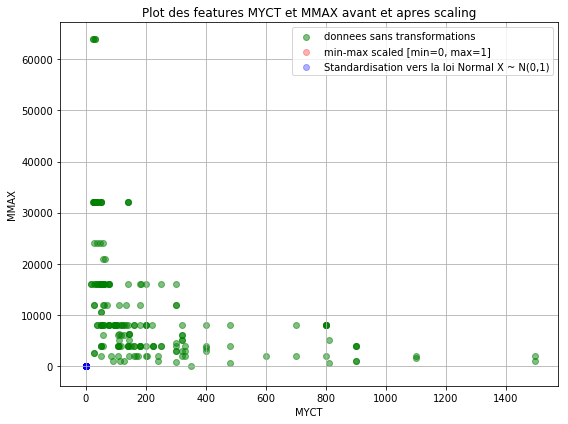
Ce jeu de données ne contient pas beaucoup d’observations (rows). Cependant, on voit bien comment les données (points verts) sont « éparpillées » dans tout le schéma. Il s’agit des données sans feature Scaling.
Après application de la Standardisation, on remarque une concentration autour du point (0,0) des données. Cela parce qu’on a réduit l’écart type des données transformées. Par ailleurs, les données du Min-Max Scaling seront aussi au niveau du point (0,0) mais « cachées » par le point en bleu.
Conclusion
Le Feature Scaling permet de préparer les données quand elles ont des échelles différentes. Faire du Feature Scaling est une bonne pratique et il permettra d’avoir de meilleurs modèles prédictifs.
Parmi les techniques du feature scaling, on retrouve la Standardisation et la Normalisation. Vous savez maintenant comment utiliser Sickit Learn pour normaliser vos features.
Je vous suggère de télécharger le code que vous venez de lire et de l’essayer chez vous. Si vous avez des questions, posez les par un commentaire et je ferai de mon mieux pour y répondre.

Merci beaucoup #Younes Benzaki pour vos articles très instructeurs et bien concis! Tout droit à l’essentiel et suivis d’exemples! Bravo 🙂
Hello Majort,
Votre commentaire a du se faufiler du coup je n’ai pas eu l’occasion de vous répondre.
Tout le plaisir est pour moi ! j’apprécie que vous appréciez mes articles 🙂
Au plaisir de vous retrouver parmi nous !
Younes
« Application de la standardisation
Pour appliquer la standardisation, on peut utiliser la classe StandardScaler de Sickit Learn.
from sklearn.preprocessing import MinMaxScaler »
Je crois qu’il y a une incohérence ici, vous n’utilisez pas standardScaler dans cette section mais MinMaxScaler ?
Oui il s’agit certainement d’une erreur.
Merci beaucoup #Younes Benzaki pour vos articles, c’est trés claires et bien expliqués bravo.
j’ai une question concernant le choix entre standardisation et normalisation? quels sont les critères pour utiliser telle ou telle méthode?
merci
Bonjour nada,
Merci pour votre commentaire 🙂
Pour répondre à votre question, il n’y pas de « réponse unique » à votre question. Le choix de l’une ou l’autre méthode se fera en fonction des données que vous avez et l’algorithme que souhaitez appliquer.
En effet, certains algorithmes « supposent » que les données en entrée sont régies par une loi normal, dans ce cas il faut standardiser les données.
La normalisation (min-max) quant à elle, permet de contraindre la plage de variation de données. En effet, les valeurs normalisées seront dans un intervalle fixe (généralement 0 et 1 mais ça peut être un autre interval). Cette technique peut être utile dans l’apprentissage depuis des images ou on veut contraindre la plage de valeurs d’un pixel à un interval [0, 255] par exemple (qui correspond au niveaux de gris d’un pixel).
Toutefois, la normalisation a pour effet de réduire ou inhiber les effets des valeurs aberrantes (outliers).