En Data Science, les jeux de données comportent souvent des irrégularités et des erreurs. Cela peut être des données manquantes ou des données aberrantes. Savoir traiter ces données permettra de produire un modèle prédictif accru et efficace.
Dans cet article, on se focalisera sur les données aberrantes. Ainsi, on verra :
- Ce que c’est une valeur aberrante (Outlier en anglais)
- Pourquoi il est important de détecter les outliers
- Comment détecter les valeurs aberrantes
- Comment réagir face aux valeurs aberrantes
C’est parti !

Qu’est ce qu’une valeur aberrante ?
Une valeur aberrante est une valeur extrême, anormalement différente de la distribution d’une variable. En d’autres termes, la valeur de cette observation diffère grandement des autres valeurs de la même variable.
Par exemple, si on prend la variable Salaire de la population française, l’ensemble des valeurs constituent une distribution de la variable Salaire. Imaginons qu’en général, pour cette distribution, les salaires varient entre 1600€ et 3000 €. Si on observe un individu avec un salaire à 10 000€, c’est une valeur extrême. On dira qu’il s’agit d’un outlier.
Dans le même sens, imaginons qu’une personne touche 200 € seulement, c’est un salaire anormalement bas. Il s’agit également d’une valeur aberrante.
Pourquoi il est important de détecter un Outlier ?
Plusieurs algorithmes de Machine Learning sont sensibles aux données d’entrainement ainsi qu’ à leurs distributions. Avoir des Outliers dans Training Set d’un algorithme de Machine Learning peut rendre la phase d’entrainement plus longue. Sans mentionner que l’apprentissage sera biaisé. Par conséquent, le modèle prédictif produit ne sera pas performant, ou du moins, loin d’être optimal.
Bien avant la phase d’apprentissage, les valeurs aberrantes influencent certains paramètres statistiques, comme la moyenne. Cela peut fausser notre compréhension du jeu de données et nous conduire à émettre des hypothèses erronées sur ce dernier. Détecter ses Outliers nous permettra de faire des suppositions plus aguerries.
Comment détecter les Outliers ?
La détection des outliers peut se faire à l’aide de méthodes de visualisation. Notamment les Box Plot et les Scatter Plot.
Détection univariée des outliers avec les Box Plot
Il s’agit de la méthode la plus simple. Les Box Plot (Boîtes à Moustaches) permettent de visualiser la distribution d’une seule variable. Ces graphiques se basent sur la mediane, ainsi que les quartiles inférieur et superieur ![]() et
et ![]() respectivement.
respectivement.
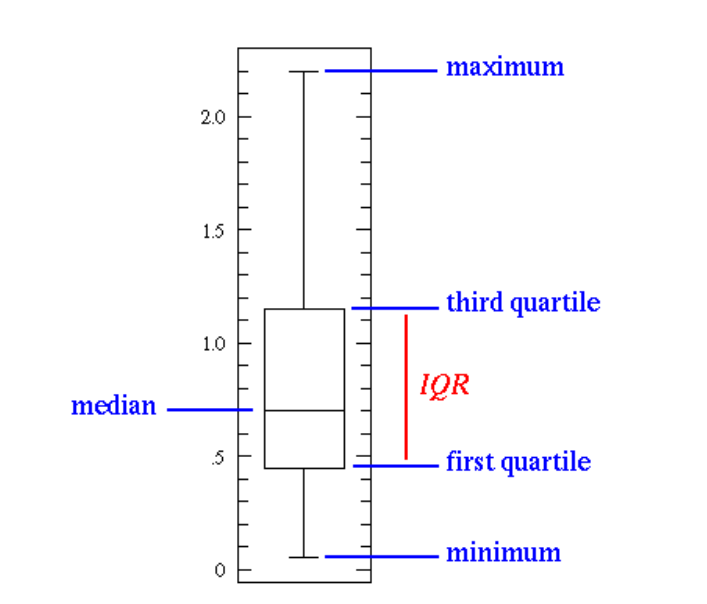
Un outlier est toute valeur extrême, supérieure ou inférieure à ![]() fois l’écart interquartile IQR. Généralement
fois l’écart interquartile IQR. Généralement ![]() vaut
vaut ![]() .
.
Détection multivariée des outliers avec les Scatter plot
Parfois, on peut être amené à vouloir détecter des valeurs aberrantes en fonction de plusieurs données. Il s’agit alors de détecter les outliers dans une relation entre variables. Cela peut être intéressant pour mettre en évidence une corrélation entre deux features.
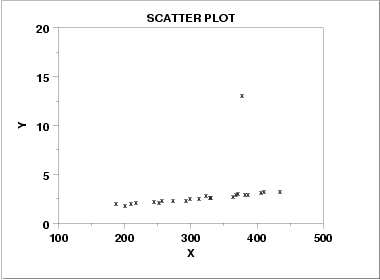
Dans cet exemple on remarque une relation linéaire entre ![]() et
et ![]() . Toutefois, on a un couple (375, 13) qui est complètement loin qui représente une valeur aberrante. On dit que cette observation est aberrante pour la corrélation observée entre les features
. Toutefois, on a un couple (375, 13) qui est complètement loin qui représente une valeur aberrante. On dit que cette observation est aberrante pour la corrélation observée entre les features ![]() et
et ![]() .
.
Comment réagir face aux valeurs aberrantes ?
Les valeurs aberrantes sont des observations extrêmes indiquant une situation extraordinaire. Dans ce sens, un outlier n’est pas forcement une valeur impertinente. Pour donner un sens à un outlier, il faut comprendre le contexte métier de la donnée.
Par conséquent, il ne faut pas les supprimer systématiquement avant d’avoir compris leur sens d’apparition dans le jeu de données.
Avant de se décider de supprimer ou garder une observation aberrante, posez- vous les questions suivantes:
- Est-ce une valeur due à une erreur de mesure ou de collecte d’information ?
- Est-ce d’un point de vue métier cette valeur est possible ?
- Si je garde cette observation, sera-t-elle bénéfique pour mon modèle prédictif ?
Valeur aberrante due à une erreur de collecte d’information
Si en regardant l’information portée par cette valeur aberrante on se rend compte que d’un point de vue sémantique, ce n’est plausible ou logique, il faudra supprimer cette valeur.
Comme exemple, prenons un jeu de données contenant des prises de températures d’eau. Si on trouve une valeur de température à 150°C, on se dira que cela est impossible. En effet, l’eau s’évapore à 100°C. Cette valeur à 150°C est donc vide de sens et faudra supprimer cette observation.
Par ailleurs, le fait de trouver dans le jeu de données, une observation de température d’eau à 150°C peut être dû à une erreur de saisie de la valeur ou une défaillance du capteur (thermomètre).
Valeur extrême mais sémantiquement plausible
Dans ce cas de figure, on se retrouve avec une donnée extrême et rare, mais plausible. Se décider de garder l’observation ou non, est plus délicat. En effet, il faut savoir dans quel contexte cette information sera utilisée (paragraphe suivant).
Comprendre le sens métier d’une variable aidera à savoir s’il faut la garder ou non
Prenons comme exemple, le salaire des citoyens américains, on aura un certain intervalle de valeurs qui nous paraîtra censé (entre 1500 et 5000 dollars par exemple). Les salaires de Bill Gates, ou Donald Trump seront forcément beaucoup plus élevés que le reste de la distribution. D’un point de vue sémantique cela est plausible bien que c’est rare. pour confirmer la rareté des salaires des gens très riches, voici un article ludique pour le prouver 🙂
Dans ce cas, le salaire des gens riches n’est pas vide de sens pour la distribution de la variable Salaire. Il indique tout simplement une observation anormalement différente mais qui est sémantiquement correcte.
Garder ou non un Outlier ?
C’est la question à 1 million d’euros ! Pourtant la réponse relève du bon sens bien qu’elle ne soit pas systématique.
Pour vous simplifier la décision, retenez ceci :
Si votre modèle prédictif est sensible aux outliers, et que vous souhaitez découvrir une pattern ou une fonction de prédiction, garder les données aberrantes biaisera votre modèle. La conséquence c’est que vous n’aurez pas un modèle optimal.
Dans ce cas, sans hésiter, supprimez ces valeurs !
Par ailleurs, si vous devez détecter des comportements anormaux comme des mouvements bancaires frauduleux ou douteux, ces outliers vous seront utiles. En effet, pour qu’un algorithme apprenne la notion de comportement anormal, il faudra qu’il les observent !
Dans ce casde figure, vous pouvez garder ces valeurs aberrantes !
En complément, lire cette article sur l’Anomaly Detection (Outliers Detection)
Conclusion
Approcher les données aberrantes n’est pas toujours évident. Il n’y a pas d’approche systématique pour les gérer. Il faut comprendre le contexte métier dans lequel elles se présentent. Cette compréhension du contexte métier est toujours souhaitable pour tout Data Scientist qui se respecte.
Si vous avez des questions concernant les outliers, n’hésitez pas à les poser en commentaire. 🙂

quelles sont les algorithmes en machine learning utilisées en ce domaine, détection outlier .
Bonjour,
Une valeur aberrante sort des valeurs « ordinaires ». Ceci en fonction de ton jeu de données. Ainsi, il vaut mieux que ce processus soit fait manuellement.
D’une part cela vous permettra de mieux comprendre vos données. Deuxièmement, cela vous donnera éventuellement, une idée sur le pourquoi tel outlier est dans ton Data set
je te propose également cet article expliquant avec des snippets de code enlever ces valeurs abérrantes (en anglais):
https://www.kdnuggets.com/2017/02/removing-outliers-standard-deviation-python.html
Bonjour,
Vous proposez d’utiliser une boxplot pour detecter des outliers dans un jeu de données. Il me semble que cette méthode est pertinente lorsque la loi mise en jeu est une loi normale. Non ? Comment utiliser cette méthode pour une distribution quelconque ? Sylvain.
Bonjour Correra,
Le box plot est une aide visuelle pour comprendre la notion de IQR (écart inter-quartile).
Quand on dispose de données ayant une forme de distribution normal (ou y ressemblant grandement), on peut utiliser les écart-types (standard deviation) pour faire une délimitation des outliers. Généralement, on convient à 2 ou 3 standard deviations à partir de la moyenne de la distribution (des deux côtés da la moyenne) pour délimtier la limite à partir de laquelle ce qui se trouve en dehors de cette limite est considéré comme valeur aberrante.
Quand on a pas des données répondant à une loi normal, la métrique IQR est pertinente pour délimiter les outliers. Dans ce sens, on considére généralement 1,5 fois le IQR comme limite pour délimiter les outliers.
Younes
Bonjour,
J’ai un jeu de données avec un code article contenant différents prix car plusieurs commandes différentes possibles.
Je souhaiterais avoir la moyenne de prix de mon code article mais en enlevant les prix qui sont très peu utilisés.
Comment faire?
Je précise que j’ai tout un fichier avec différents codes et différents prix et je dois faire de même pour chaque code article.
En vous remerciant,
Bonjour,
N’ayant pas accès aux données, je ferai des suppositions.
Si vous avez des données sur excel, il faudra grouper vos données sur le code article et par la suite calculer la moyenne sur les prix. Vous pouvez faire cela notamment via les filtres et la fonction Query de Excel.
Si vous avez les données sur une base de données SQL, la même démarche sera à appliquer notamment grâce à des fonctions d’aggregation comme le GROUP BY. Vous aurez une requête proche de ce style : select code_barre, AVG(prix) from table_des_commandes GROUP By (code_barre).
Si vous avez des données sur un CSV, vous pouvez les charger via EXCEL, ou via un script Python et utiliser Pandas pour calculer la moyenne.
Bien à vous
Bonjour,
Je suis entrain de travailler sur des données expérimentales avec quoi je suis censé établir la relation entre une variable à expliquer et une variable explicative. Le problème est que à l’issu de ma modélisation linéaire sur le logiciel JMP, j’ai exclu certaines valeurs qui pour moi, sont des valeurs aberrante. Après mon responsable aimerait que je prouve cela à travers des test de valeurs aberrante tels que Grubbs et autres. Alors que pour moi le fait que mon modèle est statisquement satisfaisant, serait suffisant. Vu que c’est seulement àprès l’exlusion de ces valeurs aberrantes, que j’ai pu avoir un R carré plus élevé et aussi des constantes sugnificatives par le test de Fisher et de Student .
J’aimerais ainsi vous solliciter si vous pensez vraiment que c’est pas scientifique le fait de les avoir exlu sans pour autant fait un test de valeurs aberrantes sur les valeures aberrantes.
Je vous remercie d’avance!
Bonjour Sareh,
J’ai l’impression que votre objectif et celui de votre responsable diverge d’ou la discordance entre vous. De ma compréhension, le responsable cherche à prouver statistiquement une corrélation entre des variables, dans ce cas il est pertinent de se conformer à la rigueur statistique car dans ce cas précis vous êtes entrain de faire des stats et non du machine Learning.
D’un autre côté, selon vos dires, j’ai l’impression que vous étiez entrain d’élaborer un modèle prédictif, dans ce cas la votre approche me semble aussi bonne car il est normal d’enlever les valeurs non-significatives afin de réduire le bruit engendré par ces dernières.
A mon avis, vos deux approchent sont bonnes selon la situation. Le plus important est de se mettre d’accord sur l’objectif à atteindre souhaité et par la suite s’accorder sur une approche.
Bon courage
Younes
bonjour,
j’aimerais confirmé des dires. Ainsi, est ce que la valeur aberrante est il responsable de la supériorité de l’écart-type par rapport à la moyenne? si c’est le cas, que dois je faire par la suite du traitement de donnée?
Addis
Bonjour,
La présence d’une valeur aberrante a surtout une incidence sur la moyenne arithmétique. Toutefois, L’écart-type, qui est une mesure de dispersion, se base sur la moyenne pour qu’il puisse être calculé. Donc oui, je dirais qu’une valeur aberrante aura un effet sur la valeur de l’écart type.
Ceci étant dit, une valeur aberrante peut être aussi bien positive que négative.
Finalement, je vous conseille cet excellent article traitant plus en détail votre question :
https://www150.statcan.gc.ca/n1/edu/power-pouvoir/ch12/5214891-fra.htm#:~:text=%C3%89cart%2Dtype%20(S)%20%3D,dispersion%20autour%20de%20la%20moyenne.
Bon courage
Younes